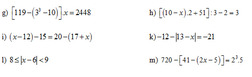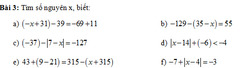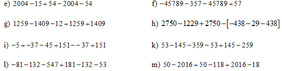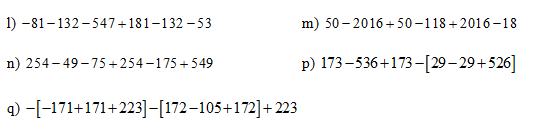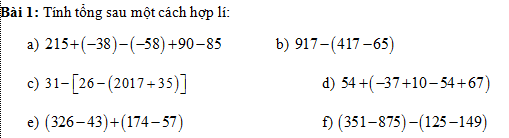\(g,\left[119-\left(3^3-10\right)\right].x=2448\\ \Leftrightarrow\left[119-\left(27-10\right)\right].x=2448\\ \Leftrightarrow\left[119-27+10\right].x=2448\\ \Leftrightarrow102.x=2448\\ \Leftrightarrow x=\dfrac{2448}{102}=24\\ h,\left[\left(10-x\right).2+51\right]:3-2=3\\ \Leftrightarrow\left[\left(10-x\right).2+51\right]:3=3+2=5\\ \Leftrightarrow\left[\left(10-x\right).2+51\right]=5.3=15\\ \Leftrightarrow\left(10-x\right).2=15-51=-36\\ \Leftrightarrow10-x=\dfrac{-36}{2}=-18\\ \Leftrightarrow x=10-\left(-18\right)=28\\ i,\left(x-12\right)-15=20-\left(17+x\right)\\ \Leftrightarrow x-12-15=20-17-x\\ \Leftrightarrow x+x=20-17+12+15\\ \Leftrightarrow2x=30\\ \Leftrightarrow x=\dfrac{30}{2}=15\)
\(k,-12-\left|13-x\right|=-21\\ \Leftrightarrow\left|13-x\right|=-12-\left(-21\right)=-12+21=9\\ \Leftrightarrow\left[{}\begin{matrix}13-x=9\\13-x=-9\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=13-9=4\\x=13-\left(-9\right)=13+9=22\end{matrix}\right.\)