Bài 1:
1.1: (x+y)+(x-y)
=x+y+x-y
=2x
1.2: \(\left(x+y\right)-\left(x-y\right)=x+y-x+y=2y\)
1.3: \(\left(x^2y+x^3-xy^2+3\right)+\left(x^3+xy^2-xy-6\right)\)
\(=x^2y+x^3-xy^2+3+x^3+xy^2-xy-6\)
\(=2x^3+x^2y-xy-3\)
1.4: \(\left(x^2-2xy+y^2-y^2\right)-\left(2xy+x^2+1\right)\)
\(=x^2-2xy-2xy-x^2-1=-4xy-1\)
1.5: \(\left(x^2-2xy+3\right)\left(-xy\right)\)
\(=-x^2\cdot xy+2xy\cdot xy-3\cdot xy\)
\(=-x^3y+2x^2y^2-3xy\)
1.6: \(\left(5x-2y\right)\left(x^2-xy+1\right)\)
\(=5x^3-5x^2y+5x-2x^2y+2xy^2+2y\)
\(=5x^3+5x-7x^2y+2xy^2+2y\)
1.7: \(3x\left(12x-4y\right)-2x\left(4x-3y\right)+8x^3\)
\(=36x^2-12xy-8x^2+6xy+8x^3\)
\(=8x^3+28x^2-6xy\)
1.8: \(\left(5x^4y^3-x^3y^2+2x^2y\right):\left(-x^2y\right)\)
\(=-\dfrac{5x^4y^3}{x^2y}+\dfrac{x^3y^2}{x^2y}-\dfrac{2x^2y}{x^2y}\)
\(=-5x^2y^2+xy-2\)
1.9: \(\left(\dfrac{1}{2}x-y\right)\left(2x-3y\right)\)
\(=x^2-\dfrac{3}{2}xy-2xy+3y^2=x^2-\dfrac{7}{2}xy+3y^2\)
1.10:\(\left[\left(2x^2y\right)^2+3x^4y^3-6x^3y^2\right]:\left(xy\right)^2\)
\(=\dfrac{4x^4y^2+3x^4y^3-6x^3y^2}{x^2y^2}\)
\(=4x^2+3x^2y-6x\)
Bài 2:
2.1:
\(A=\left(x^2+3xy-3x^3\right)+\left(2y^3-xy+3x^3\right)-y^3\)
\(=x^2+3xy-3x^3+2y^3-xy+3x^3-y^3\)
\(=x^2+2xy+y^3\)
Thay x=5;y=4 vào A, ta được:
\(A=5^2+2\cdot5\cdot4+4^3=25+40+64=129\)
2.2:
\(B=x^2\left(x+y\right)-y\left(x^2-y^2\right)=x^3+x^2y-x^2y+y^3=x^3+y^3\)
Thay x=-6;y=8 vào B, ta được:
\(B=\left(-6\right)^3+8^3=-216+512=296\)
2.3:\(C=\left(2x-y\right)\left(x-y\right)+y^2\)
\(=2x^2-2xy-xy+y^2+y^2=2x^2-3xy+2y^2\)
Thay x=-1;y=1 vào C, ta được:
\(C=2\cdot\left(-1\right)^2-3\cdot\left(-1\right)\cdot1+2\cdot1^2\)
=2+3+2
=7
2.4: \(D=\left(x-5\right)\left(x+2\right)+\left(x+1\right)\left(2-x\right)\)
\(=x^2+2x-5x-10+2x-x^2+2-x\)
=-2x-8
Thay x=3 vào D, ta được:
\(D=-2\cdot3-8=-6-8=-14\)
2.5:
\(E=x\left(2-y\right)\left(x^2+x-5\right)\)
\(=\left(2x-xy\right)\left(x^2+x-5\right)\)
\(=2x^3+2x^2-10x-x^3y-x^2y+5xy\)
Thay x=2;y=-1 vào E, ta được:
\(E=2\cdot\left[2-\left(-1\right)\right]\left(2^2+2-5\right)=2\cdot3\cdot\left(4+2-5\right)=6\)
2.6:
\(F=\left(y+2\right)\left(x^2-3\right)+\left(y-1\right)\left(7-5x\right)-7x^2\)
\(=x^2y-3y+2x^2-6+7y-5xy-7+5x-7x^2\)
\(=-5x^2+x^2y+4y-5xy+5x-13\)
Thay x=-5;y=1 vào F, ta được:
\(F=\left(1+2\right)\left[\left(-5\right)^2-3\right]+\left(1-1\right)\left(7-5\cdot\left(-5\right)\right)-7\cdot\left(-5\right)^2\)
\(=3\cdot\left[25-3\right]-7\cdot25\)
=66-175
=-109
2.7: \(G=125x^9y^5z^2:\left(-5x^7y^4z\right)\)
\(=-\dfrac{125x^9y^5z^2}{5x^7y^4z}=-25x^2yz\)
Thay x=8;y=-2;z=-1 vào G, ta được:
\(G=-25\cdot8^2\cdot\left(-2\right)\cdot\left(-1\right)=-50\cdot64=-3200\)
2.8: \(C=\left(-x^3y^3\right)^4:\left(-x^{12}y^{11}\right)\)
\(=\dfrac{x^{12}y^{12}}{-x^{12}y^{11}}=-y\)
Khi y=-4/3 thì \(C=-y=-\left(-\dfrac{4}{3}\right)=\dfrac{4}{3}\)

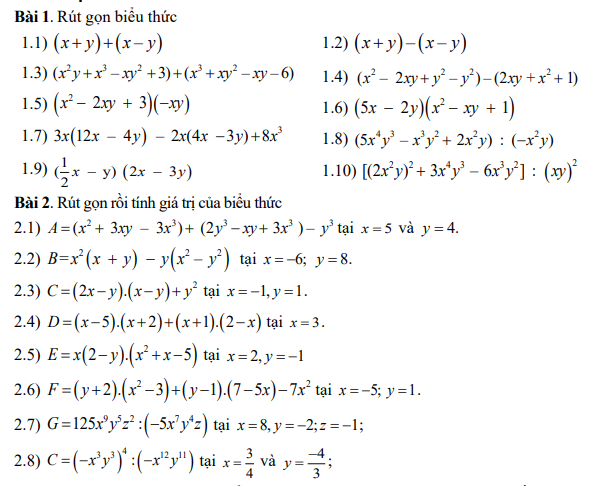 giúp giupvới ạ
giúp giupvới ạ




 Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!



 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ



