Câu a chỉ chứng minh được 2 tam giác đồng dạng thôi nha!
\(a,\left\{{}\begin{matrix}\widehat{FHC}=\widehat{AHE}\left(đối.đỉnh\right)\\\widehat{FHC}+\widehat{FCH}=90^0\\\widehat{AHE}+\widehat{EAH}=90^0\end{matrix}\right.\Rightarrow\widehat{FCH}=\widehat{EAH}\)
Ta có BD,CE là 2 đường cao giao tại H nên H là trực tâm tam giác ABC
\(\Rightarrow AF\) là đường cao thứ 3
\(\left\{{}\begin{matrix}\widehat{AFB}=\widehat{CFH}\left(=90^0\right)\left(1\right)\\\widehat{FCH}=\widehat{EAH}\left(cm.trên\right)\left(2\right)\end{matrix}\right.\Rightarrow\Delta FAB\sim\Delta FCH\left(g.g\right)\)
\(b,\) Ta có \(AB=CH\) kết hợp với \((1)\) và \((2)\)
\(\Rightarrow\Delta FAB=\Delta FCH\left(ch-gn\right)\\ \Rightarrow AF=FC\)
Mà \(\widehat{AFC}=90^0\Rightarrow\Delta AFC\) vuông cân tại C
Vậy \(\widehat{ACB}=45^0\)






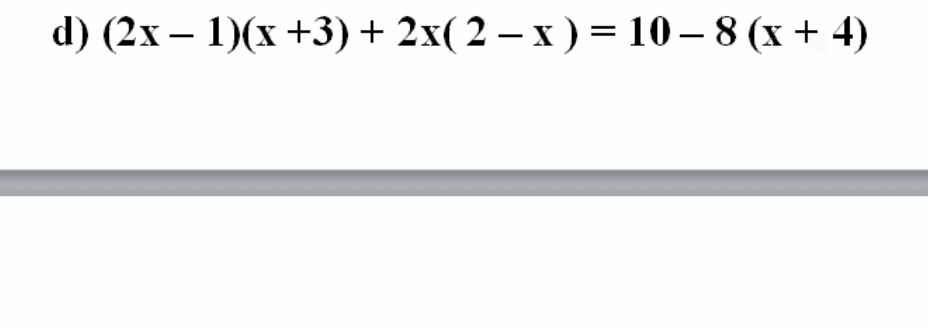 Giúp em vs ạ ! Em camon.
Giúp em vs ạ ! Em camon. 
 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ











