a,b \(\in\) Z, a \(\ne\) b, b > 0
So sánh: \(\dfrac{a}{b}\) và \(\dfrac{a+2022}{b+2022}\)
Có hai trường hợp:
+ Nếu a < b ta có:
\(\dfrac{a}{b}\) = 1 - \(\dfrac{b-a}{b}\) ; \(\dfrac{a+2022}{b+2022}\) = 1 - \(\dfrac{b-a}{b+2022}\)
Vì \(\dfrac{b-a}{b}\) > \(\dfrac{b-a}{b+2022}\)
Vậy : \(\dfrac{a}{b}\) < \(\dfrac{a+2022}{b+2022}\)
+ Nếu a > b ta có
\(\dfrac{a}{b}\) = 1 + \(\dfrac{a-b}{b}\); \(\dfrac{a}{b}\) = 1 + \(\dfrac{a-b}{b+2022}\)
Vì \(\dfrac{a-b}{b}\) > \(\dfrac{a-b}{b+2022}\)
Vậy \(\dfrac{a}{b}\) > \(\dfrac{a+2022}{b+2022}\)


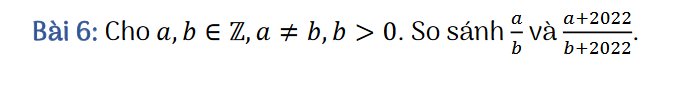



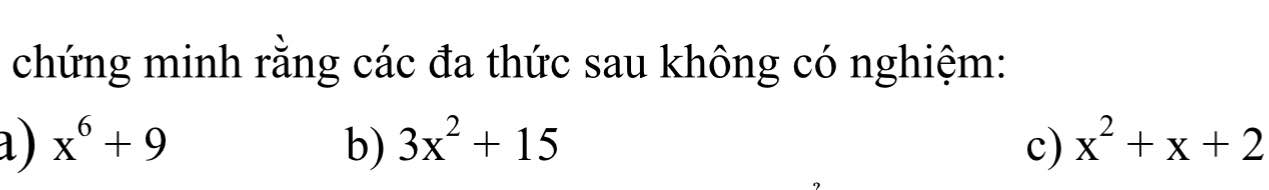





 MMÌnh đag cần giải chi tiết 4 phần . Mình đag cần rất gấp. Mn giúp mình vớiiiiiiiii
MMÌnh đag cần giải chi tiết 4 phần . Mình đag cần rất gấp. Mn giúp mình vớiiiiiiiii