\(\dfrac{4n-1}{n-1}=\dfrac{4n-4+3}{n-1}=\dfrac{4\left(n-1\right)+3}{n-1}=\dfrac{4\left(n-1\right)}{n-1}+\dfrac{3}{n-1}=4+\dfrac{3}{n-1}\)
Để nguyên thì \(n-1\in U\left(3\right)=\left\{\pm1;\pm3\right\}\)
n-1=1 => n=2
n-1=-1 =>n=0
n-1=3 => n=4
n-1=-3 => n=-2
ĐK:x\(\ne\)1
\(\dfrac{4n-1}{n-1}=\dfrac{4n-4+3}{n-1}=\dfrac{4\left(n-1\right)+3}{n-1}=4+\dfrac{3}{n-1}\)
Để \(\dfrac{4n-1}{n-1}\in Z\Rightarrow\dfrac{3}{n-1}\in Z\Rightarrow3⋮\left(n-1\right)\Rightarrow n-1\inƯ\left(3\right)\)
Ta có bảng:
| n-1 | -3 | -1 | 1 | 3 |
| n | -2 | 0 | 2 | 4 |
Vậy \(n\in\left\{-2;0;2;4\right\}\)







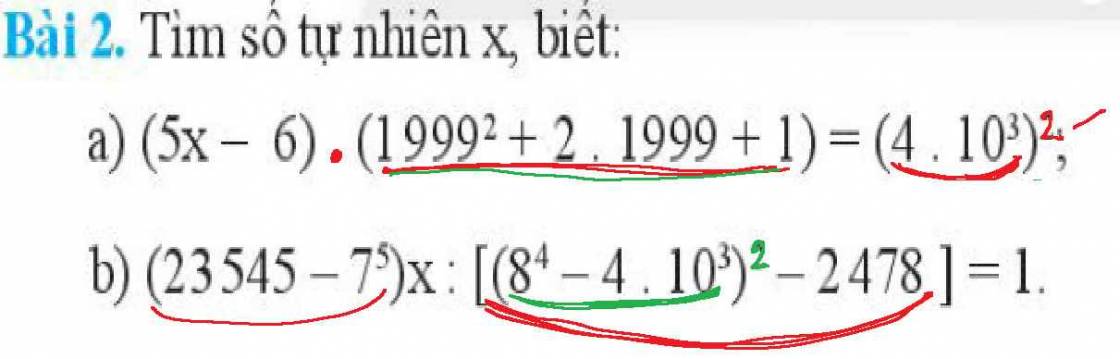




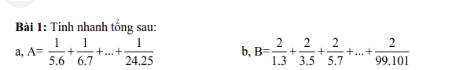


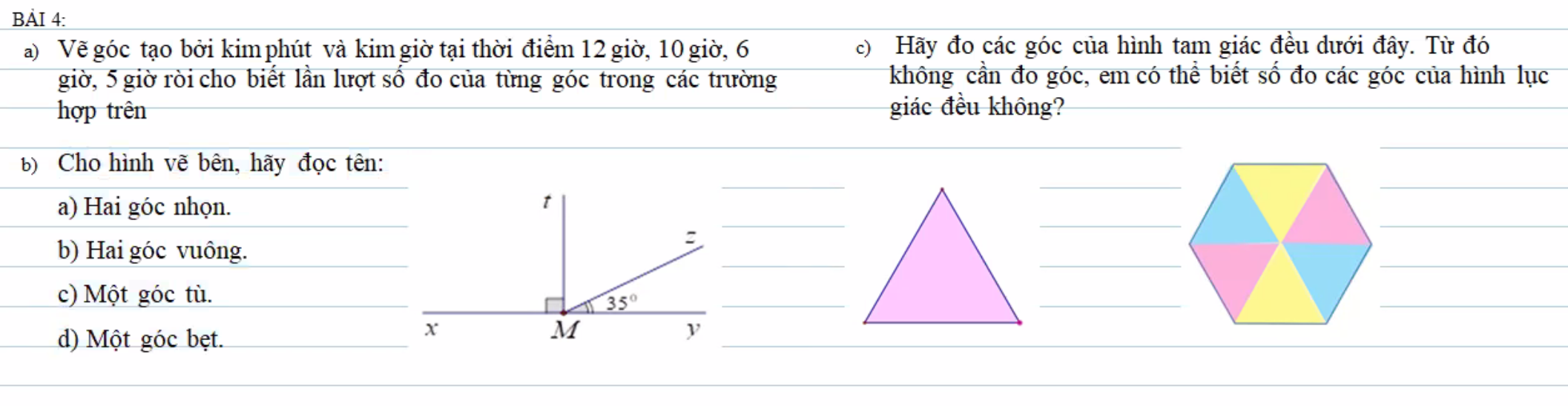

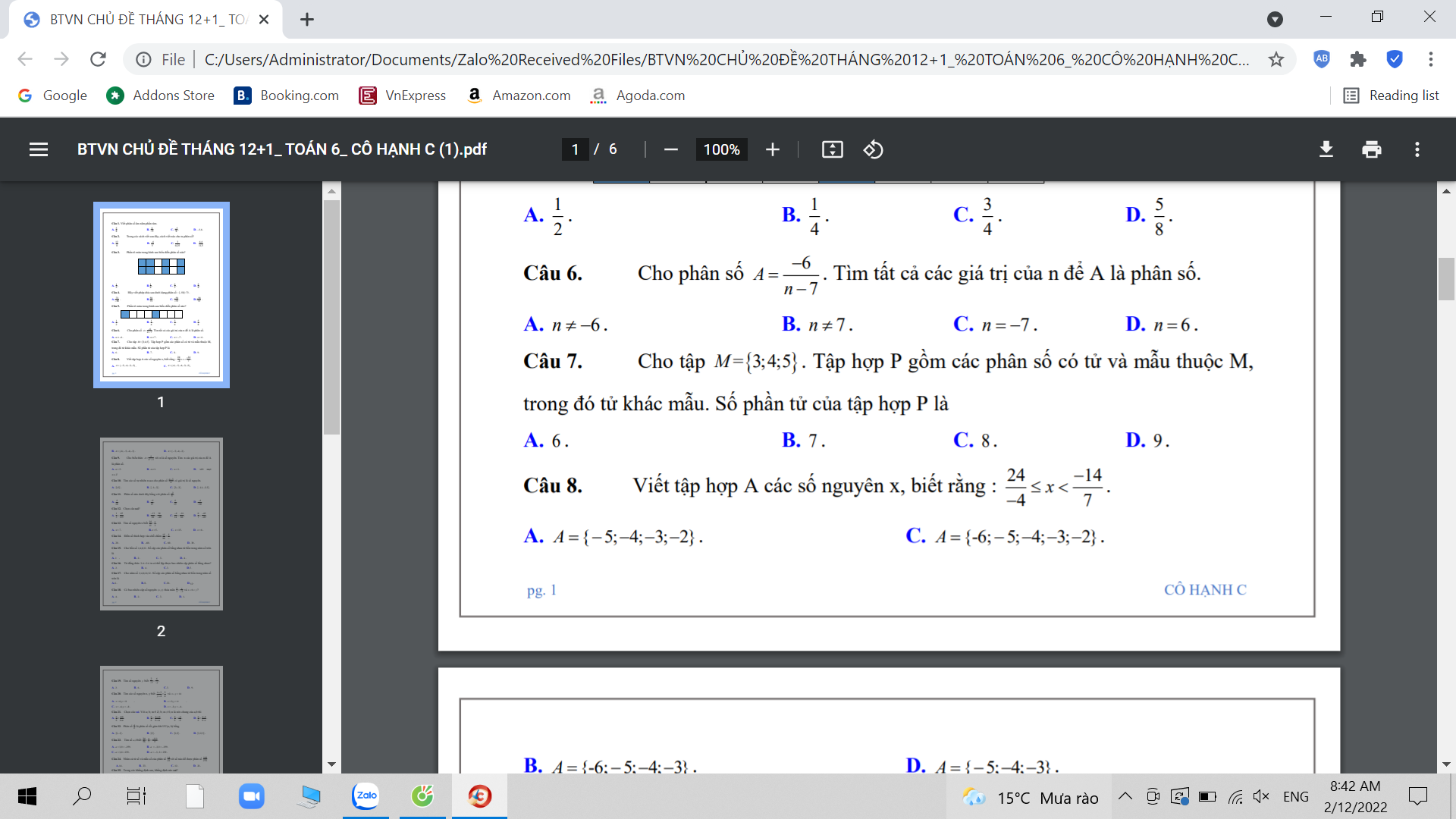 mọi người giúp em với ạ em đang cần gấp!!
mọi người giúp em với ạ em đang cần gấp!!
