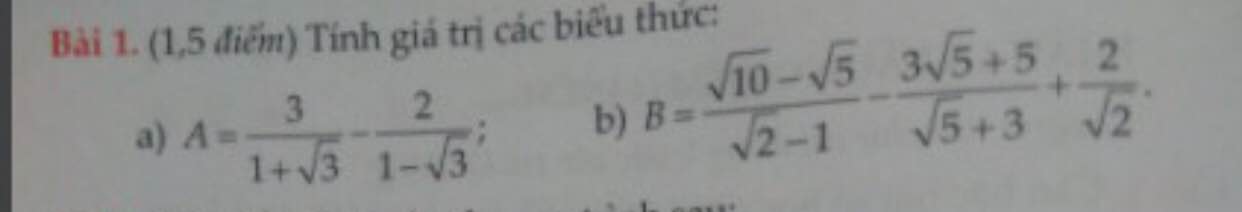a)
\(A=\dfrac{3}{\sqrt{3}+1}+\dfrac{2}{\sqrt{3}-1}=\dfrac{3\left(\sqrt{3}-1\right)}{3-1}+\dfrac{2\left(\sqrt{3}+1\right)}{3-1}=\dfrac{3}{2}\left(\sqrt{3}-1\right)+\sqrt{3}+1=\dfrac{3\sqrt{3}}{2}-\dfrac{3}{2}+\sqrt{3}+1=\dfrac{5\sqrt{3}}{2}-\dfrac{1}{2}\)
b)
\(B=\dfrac{\sqrt{5}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}-\dfrac{\sqrt{5}\left(3+\sqrt{5}\right)}{\sqrt{5}+3}+\dfrac{2\sqrt{2}}{2}=\sqrt{5}-\sqrt{5}+\dfrac{2\sqrt{2}}{2}=\dfrac{2\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
giúp em với ạ em đang cần gấp mn giúp em 
Giúp em với ạ, làm cụ thể giúp em. Em cảm ơn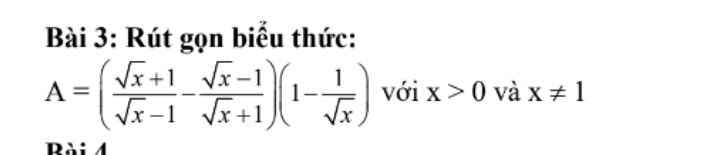
Ai giúp em với em đang cần gấp làm hết giúp em ạ
Giúp em với ạ em đang cần gấp . Làm hết giúp em nha 
Giúp em với ạ! Em đang cần gấp lắm nên mong mọi người giúp em
Giúp em với ạ vẽ giúp em câu A ạ
 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Giúp em với ạ giúp em nhanh lên nha mn 🥺
Giúp em câu A với câu C giải nhanh giúp em ạ 
Mọi người giúp em viết giải thích, kết luận giúp em với