Bài 1:
a: \(M=\left(\dfrac{x^2-1}{x^4-x^2+1}-\dfrac{1}{x^2+1}\right)\left(x^4+\dfrac{1-x^4}{1+x^2}\right)\)
\(=\dfrac{\left(x^2-1\right)\left(x^2+1\right)-x^4+x^2-1}{\left(x^2+1\right)\left(x^4-x^2+1\right)}\cdot\left(x^4+\dfrac{\left(1-x^2\right)\left(1+x^2\right)}{1+x^2}\right)\)
\(=\dfrac{x^4-1-x^4+x^2-1}{\left(x^2+1\right)\left(x^4-x^2+1\right)}\left(x^4-x^2+1\right)\)
\(=\dfrac{x^2-2}{x^2+1}\)
b: \(M=\dfrac{x^2-2}{x^2+1}=\dfrac{x^2+1-3}{x^2+1}=1-\dfrac{3}{x^2+1}\)
\(x^2+1>=1\forall x\)
=>\(\dfrac{3}{x^2+1}< =3\forall x\)
=>\(-\dfrac{3}{x^2+1}>=-3\forall x\)
=>\(M=-\dfrac{3}{x^2+1}+1>=-2\forall x\)
Dấu '=' xảy ra khi x=0
Bài 3:
a: \(x^2-2005x-2006=0\)
=>\(x^2-2006x+x-2006=0\)
=>(x-2006)(x+1)=0
=>\(\left[{}\begin{matrix}x=2006\\x=-1\end{matrix}\right.\)
b: \(\left|x-2\right|+\left|x-3\right|+\left|2x-8\right|=9\)(1)
TH1: x<2
(1) sẽ trở thành: 2-x+3-x+8-2x=9
=>-4x+13=9
=>-4x=-4
=>x=1(nhận)
TH2: 2<=x<3
(2) trở thành:
x-2+3-x+8-2x=9
=>-2x+9=0
=>x=0(loại)
TH3: 3<=x<4
(1) sẽ trở thành:
x-2+x-3+8-2x=9
=>3=9(vô lý)
TH4: x>=4
(1) sẽ trở thành:
x-2+x-3+2x-8=9
=>4x-13=9
=>4x=22
=>x=5,5(nhận)
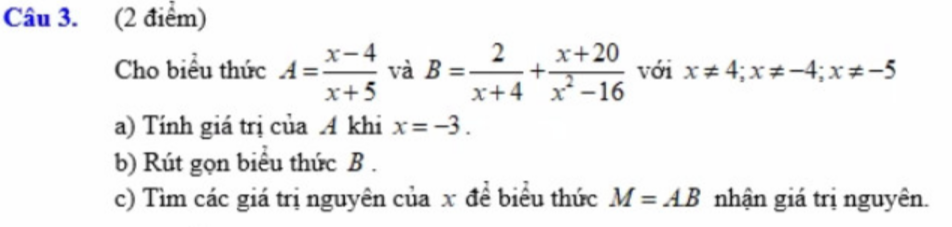
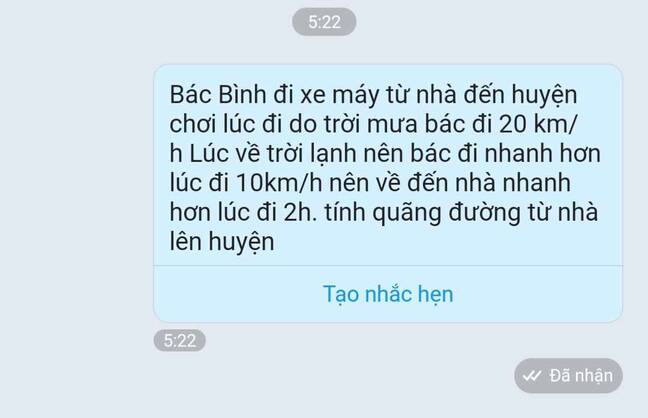Mọi người ơi giúp em với ạ, em đang cần gấp, thanks mn
