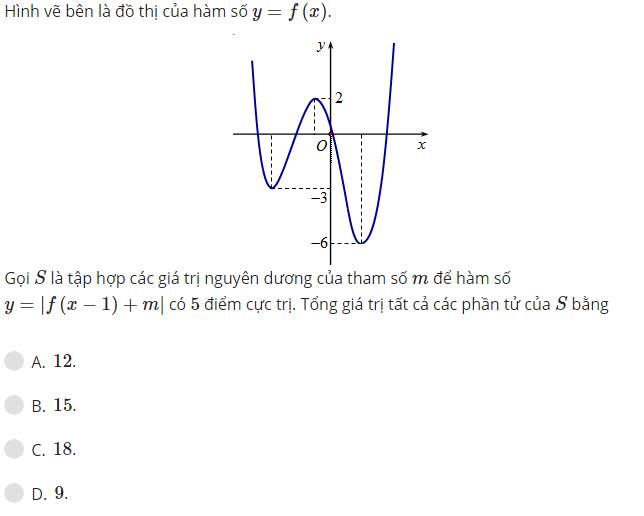
Đồ thị hàm số \(y=f\left(x-1\right)+m\) là do tịnh tiến đồ thị hàm số \(\text{y = f(x)}\) sang trái \(1\) đơn vị và lên trên \(m\) đơn vị, số điểm cực trị của đồ thị mới không thay đổi.
Để hàm số \(y=\left|f(x-1)+m\right|\) có 5 điểm cực trị, ta cần tạo thêm 2 điểm cực trị mới, 2 điểm mới đối xứng điểm có tung độ \(-3\) và \(-6\) của đồ thị \(y=f\left(x\right)\) qua trục \(Ox\) và tung độ cực đại và cực tiểu của hàm số \(y=f\left(x\right)\) là \(y_{max}=2;y_{min}=-6\), nên đồ thị hàm số \(y=\left|f(x-1)+m\right|\) sẽ có 5 điểm cực trị khi ta tịnh tiến lên trên hơn 6 đơn vị có nghĩa là \(2< m< 6\)
\(S=m\in\left\{1;2;3;4;5\right\}\left(m\in Z^+\right)\)
Tổng các phần tử của \(S\) là \(1+2+3+4+5=15\)
Chọn câu B
Câu 2 :
\(y=f\left(x\right)=\left(x-2\right)^2\left(x^2-4x+3\right),\forall x\in R\)
\(y=f\left(x^2-10x+m+9\right)\)
\(\Rightarrow y'=f\left(x^2-10x+m+9\right).\left(x^2-10x+m+9\right)'\)
\(=(x^2-10x+m+9-2)^2[(x^2-10x+m+9)^2-4(x^2-10x+m+9)+3].(2x-10)\)
Để hàm số có \(5\) điểm cực trị thì \(y'=0\) phải có \(4\) nghiệm đơn phân biệt
\(\Leftrightarrow\) \((x^2-10x+m+9-2)^2[(x^2-10x+m+9)^2-4(x^2-10x+m+9)+3]=0\) có 3 nghiệm phân biệt vì \(2x-10\ne0\) với các nghiệm của phương trình trên
Đặt \(t=x^2-10x+m+9\left(1\right)\)
\(Pt\Leftrightarrow\) \((t-2)²(t²-4t+3) = 0\)
\(\Leftrightarrow\)\((t-1)(t-2)(t-3)² = 0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=1\\t=2\\t=3\end{matrix}\right.\)
Nên (1) sẽ có nghiệm duy nhất trong 3 trường hợp
Trường hợp 1: \(t = x²-10x+m+9 = 1\) \(\Leftrightarrow\) \(x²-10x+m+8 = 0\) Để phương trình có nghiệm duy nhất thì \(Δ = 100 - 4(m+8) = 0\)\(\Leftrightarrow m=17\)
Trường hợp 2: \(t = x²-10x+m+9 = 2\) \(\Leftrightarrow\) \(x²-10x+m+7 = 0\) Để phương trình có nghiệm duy nhất thì \(Δ = 100 - 4(m+7) = 0\)\(\Leftrightarrow m=18\)
Trường hợp 3: \(t = x²-10x+m+9 = 3\) \(\Leftrightarrow\) x²-10x+m+6 = 0 Để phương trình có nghiệm duy nhất thì \(Δ = 100 - 4(m+6) = 0\) \(\Leftrightarrow m=19\)
Vậy với \(m\in\left\{17;18;19\right\}\) thỏa mãn đề bài