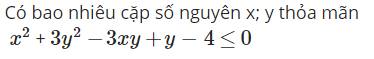a: Xét ΔAMN có
O,O' lần lượt là trung điểm của AM,AN
=>OO' là đường trung bình của ΔAMN
=>OO'//MN và MN=2O'O
b: Xét (O) có
ΔABM nội tiếp
AM là đường kính
Do đó: ΔABM vuông tại B
=>AB\(\perp\)BM
Xét (O') có
ΔABN nội tiếp
AN là đường kính
Do đó: ΔABN vuông tại B
=>AB\(\perp\)BN
\(\widehat{MBN}=\widehat{MBA}+\widehat{NBA}=90^0+90^0=180^0\)
=>M,B,N thẳng hàng
Gọi I là trung điểm của AB
=>AB là đường kính của (I)
Xét (I) có
IB là bán kính
MN\(\perp\)IB tại B
Do đó: MN là tiếp tuyến của (I)
=>MN tiếp xúc với đường tròn đường kính AB
Đúng 2
Bình luận (2)
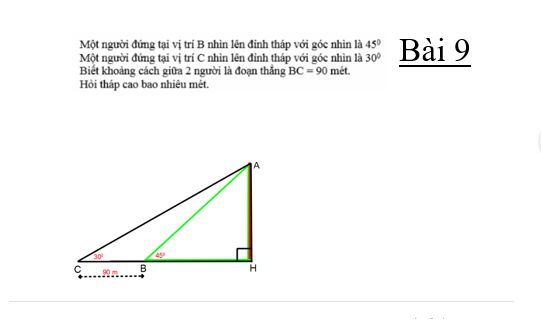giúp em với ạ. Em cảm ơn ạ
