Bài này có nhiều cách chứng minh:
Ví dụ:
Áp dụng BĐT Co-si:
\(a+b+c\ge3\sqrt[3]{abc}\)
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge3\sqrt[3]{\dfrac{1}{abc}}\)
Nhân vế với vế:
\(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\dfrac{1}{abc}}=9\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
Hoặc là cách khác:
\(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=3+\dfrac{a}{b}+\dfrac{a}{c}+\dfrac{b}{a}+\dfrac{b}{c}+\dfrac{c}{a}+\dfrac{c}{b}\ge3+6\sqrt[6]{\dfrac{a}{b}.\dfrac{a}{c}.\dfrac{b}{a}.\dfrac{b}{c}.\dfrac{c}{a}.\dfrac{c}{b}}=9\)

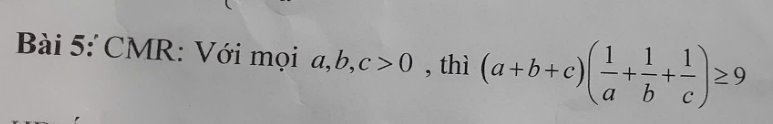








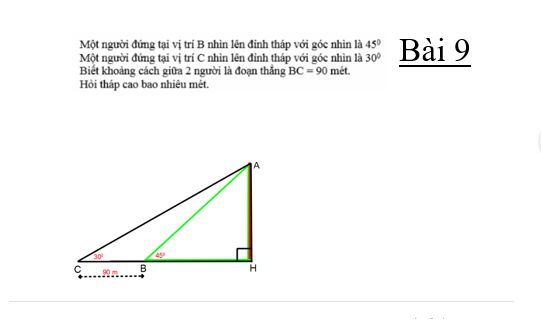 giúp em với ạ. Em cảm ơn ạ
giúp em với ạ. Em cảm ơn ạ