a: Xét tứ giác OFGE có
OF//GE
OE//FG
Do đó: OFGE là hình bình hành
=>\(\widehat{EGF}+\widehat{EOF}=180^0\)
=>\(\widehat{EGF}=180^0-90^0=90^0\)
b: OP là phân giác của góc EOF
=>\(\widehat{EOP}=\widehat{FOP}=\dfrac{\widehat{EOF}}{2}=\dfrac{90^0}{2}=45^0\)
Ta có: EG//OF
=>\(\widehat{EPO}=\widehat{POQ}=45^0\)
c: GQ là phân giác của góc EGF
=>\(\widehat{EGQ}=\dfrac{\widehat{EGF}}{2}=\dfrac{90^0}{2}=45^0\)
Ta có: \(\widehat{EPO}=\widehat{EGQ}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên OP//GQ


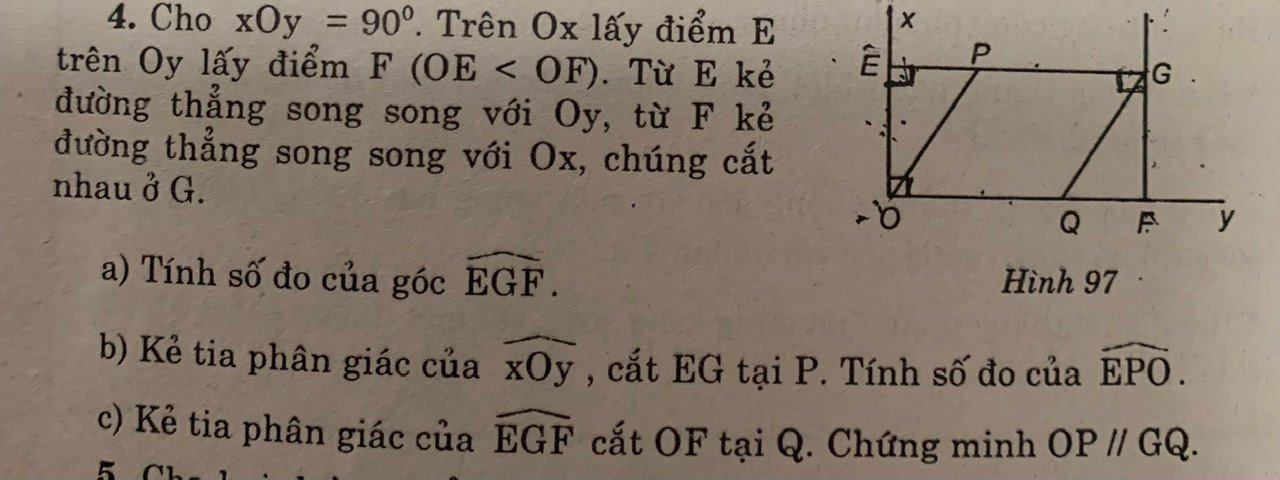




 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ

 giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ




 giúp em với ạ nhanh em cần ạ :33
giúp em với ạ nhanh em cần ạ :33 giúp em với ạ em đang cần gấp ạ
giúp em với ạ em đang cần gấp ạ giúp em với ạ em đang cần gấp ạ :(
giúp em với ạ em đang cần gấp ạ :(