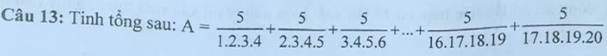Lời giải:
\(A=\frac{5}{3}\left(\frac{3}{1.2.3.4}+\frac{3}{2.3.4.5}+\frac{3}{3.4.5.6}+....+\frac{3}{16.17.18.19}+\frac{3}{17.18.19.20}\right)\\ =\frac{5}{3}\left(\frac{4-1}{1.2.3.4}+\frac{5-2}{2.3.4.5}+\frac{6-3}{3.4.5.6}+....+\frac{19-16}{16.17.18.19}+\frac{20-17}{17.18.19.20}\right)\)
\(=\frac{5}{3}\left(\frac{1}{1.2.3}-\frac{1}{2.3.4}+\frac{1}{2.3.4}-\frac{1}{3.4.5}+\frac{1}{3.4.5}-\frac{1}{4.5.6}+....+\frac{1}{16.18.18}-\frac{1}{17.18.19}+\frac{1}{17.18.19}-\frac{1}{18.19.20}\right)\)
\(=\frac{5}{3}(\frac{1}{1.2.3}-\frac{1}{18.19.20})=\frac{1139}{4104}\)
Đúng 1
Bình luận (0)
