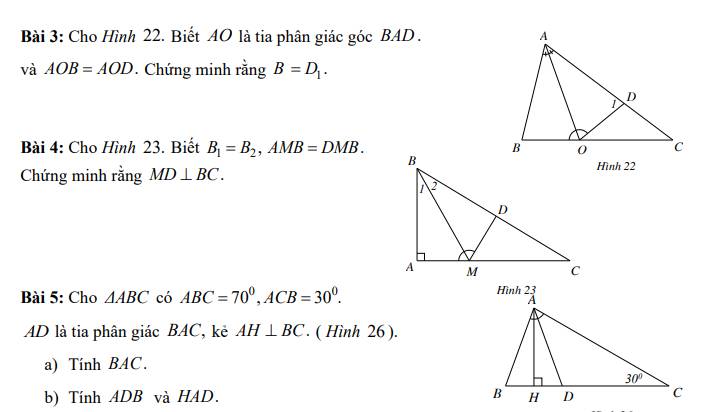
3:
Xét ΔABO và ΔADO có
\(\widehat{AOB}=\widehat{AOD}\)
OA chung
\(\widehat{BAO}=\widehat{DAO}\)
Do đó: ΔABO=ΔADO
=>\(\widehat{ABO}=\widehat{ADO}\)(ĐPCM)
Bài 4:
Xét ΔBAM và ΔBDM có
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
\(\widehat{AMB}=\widehat{DMB}\)
Do đó: ΔBAM=ΔBDM
=>\(\widehat{BAM}=\widehat{BDM}=90^0\)
=>DM\(\perp\)BC
5:
a: Xét ΔBAC có
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{BAC}=180^0-70^0-30^0=80^0\)
b: AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{80^0}{2}=40^0\)
Xét ΔADC có góc ADB là góc ngoài tại đỉnh D
nên \(\widehat{ADB}=\widehat{DAC}+\widehat{C}=40^0+30^0=70^0\)
ΔAHD vuông tại H
=>\(\widehat{HAD}+\widehat{HDA}=90^0\)
=>\(\widehat{HAD}=90^0-70^0=20^0\)





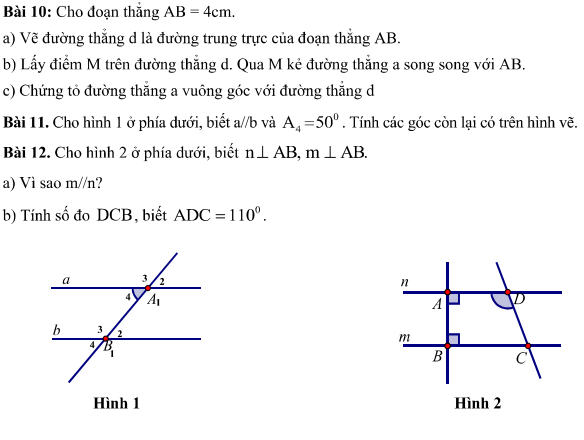


 mọi nguời giúp em gấp với ạ,chiều em phải nộp rồi,không cần hình đâu ạ!em cảm ơn !
mọi nguời giúp em gấp với ạ,chiều em phải nộp rồi,không cần hình đâu ạ!em cảm ơn !
 ai cứu em với ạ em cần nộp trc 7h10 ạ
ai cứu em với ạ em cần nộp trc 7h10 ạ


 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ

 giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ