a) Ta có: \(a^2+b^2+c^2=\left(a+b+c\right)^2-2\left(ab+bc+ca\right)=6^2-2.9=18\)
Lại có: \(a^2+b^2\ge\dfrac{\left(a+b\right)^2}{2}=\dfrac{\left(6-c\right)^2}{2}\),
suy ra \(\dfrac{\left(6-c\right)^2}{2}+c^2\le18\)
\(\Leftrightarrow\left(6-c\right)^2+2c^2\le36\)
\(\Leftrightarrow3c^2-12c\le0\)
\(\Leftrightarrow3c\left(c-4\right)\le0\Leftrightarrow0\le c\le4\)
Chứng minh tương tự, ta cũng có \(0\le b\le4;0\le a\le4\)
b) Ta có: \(2=a^2+b^2+c^2\ge\dfrac{\left(a+b\right)^2}{2}+c^2=\dfrac{\left(2-c\right)^2}{2}+c^2\)
\(\Rightarrow\left(2-c\right)^2+2c^2\le4\)
\(\Leftrightarrow3c^2-4c\le0\) \(\Leftrightarrow0\le c\le\dfrac{4}{3}\)
Chứng minh tương tự, ta cũng có \(0\le b\le\dfrac{4}{3};0\le a\le\dfrac{4}{3}\)
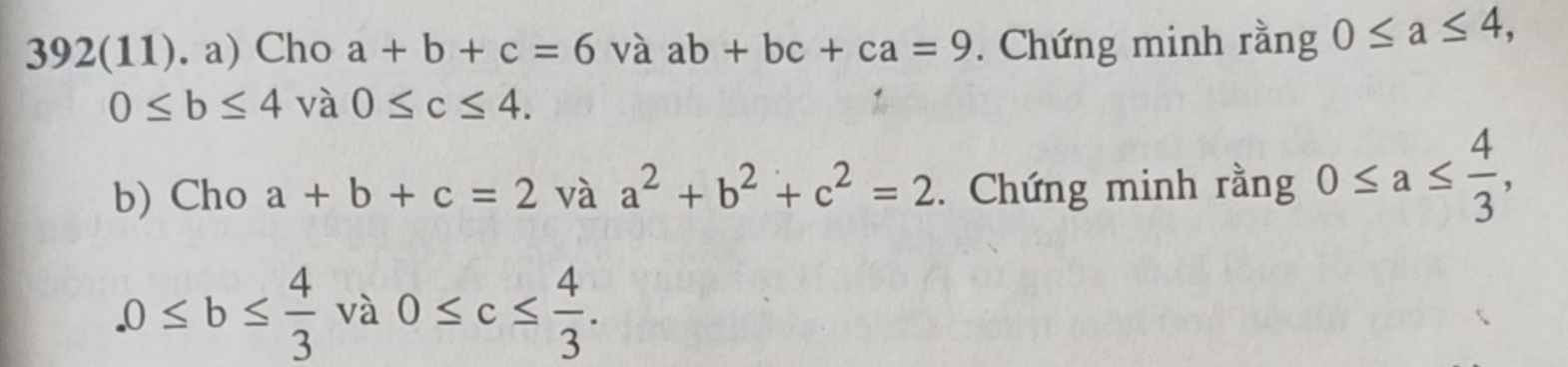
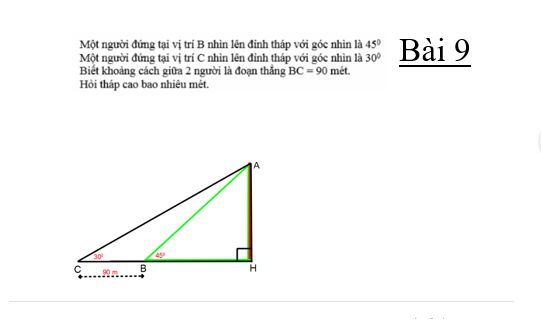giúp em với ạ. Em cảm ơn ạ
