1.
a. Câu này chắc đề ghi nhầm, biểu thức B thường chỉ tính sau khi rút gọn. Chưa rút gọn phức tạp như vậy thay số sao nổi. Tính A thì đúng hơn.
b.
\(B=\left(\dfrac{2x+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right).\left(\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}+1}-\sqrt{x}\right)\)
\(=\left(\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right).\left(x-2\sqrt{x}+1\right)\)
\(=\dfrac{1}{\sqrt{x}-1}.\left(\sqrt{x}-1\right)^2=\sqrt{x}-1\)
Bây giờ quay lại câu a, \(x=7-\sqrt{48}=\left(2-\sqrt{3}\right)^2\Rightarrow B=\sqrt{\left(2-\sqrt{3}\right)^2}-1=3-\sqrt{3}\)
c.
\(P=A+B=\dfrac{2-2\sqrt{x}}{\sqrt{x}}+\sqrt{x}-1=\dfrac{2}{\sqrt{x}}+\sqrt{x}-3\)
P nguyên khi \(\sqrt{x}\) nguyên đồng thời \(\dfrac{2}{\sqrt{x}}\) nguyên
\(\Rightarrow\sqrt{x}=Ư\left(2\right)=\left\{1;2\right\}\) (do \(\sqrt{x}>0\))
\(\Rightarrow x=\left\{1;4\right\}\)
II.1
Gọi giá niêm yết của 1 cái bàn ủi là x ngàn đồng (0<x<850)
Giá niêm yết của 1 cái quạt điện là \(850-x\) ngàn đồng
Số tiền được giảm khi mua bàn ủi: \(10\%.x=0,1x\) (ngàn đồng)
Số tiền được giảm khi mua quạt điện: \(\left(850-x\right).20\%=0,2\left(850-x\right)\) (ngàn đồng)
Do anh được giảm 125 ngàn khi mua 2 sản phẩm nên ta có pt:
\(0,1x+0,2\left(850-x\right)=125\)
\(\Leftrightarrow-0,1x=-45\)
\(\Leftrightarrow x=450\) ngàn đồng
Vậy chênh lệch giá của mỗi chiếc bàn ủi là \(0,1.450=45\) ngàn đồng và của quạt điện là \(0,2.\left(850-x\right)=80\) ngàn đồng
III.1
Đặt \(\left|x+1\right|=z\) ta được:
\(\left\{{}\begin{matrix}z+y=6\\z=4y-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}z+y=6\\z-4y=-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5y=10\\z=6-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\z=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\\left|x+1\right|=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\\left[{}\begin{matrix}x+1=4\\x+1=-4\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\end{matrix}\right.\)
Vậy hệ có 2 nghiệm: \(\left(x;y\right)=\left(3;2\right);\left(-5;2\right)\)
IV.
a.
Do AB, AC là các tiếp tuyến \(\Rightarrow\) \(\widehat{ABO}=\widehat{ACO}=90^0\)
\(\Rightarrow B,C\) cùng nhìn AO dưới 1 góc vuông nên ABOC nội tiếp
b.
Theo t/c hai tiếp tuyến cắt nhau có \(AB=AC\)
Đồng thời \(OB=OC=R\)
\(\Rightarrow AO\) là trung trực BC \(\Rightarrow AO\) vuông góc BC tại H và H là trung điểm BC
Áp dụng hệ thức lượng trong tam giác vuông OAB với đường cao BH:
\(AB^2=AH.AO\) (1)
Xét hai tam giác ABM và ANB có:
\(\left\{{}\begin{matrix}\widehat{BAM}-chung\\\widehat{ABM}=\widehat{ANB}\left(\text{cùng chắn BM}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABM\sim\Delta ANB\left(g.g\right)\Rightarrow\dfrac{AB}{AN}=\dfrac{AM}{AB}\)
\(\Rightarrow AB^2=AM.AN\) (2)
(1);(2) \(\Rightarrow AM.AN=AH.AO\)
c.
Theo t/c hai tiếp tuyến cắt nhau ta có AO là phân giác góc \(\widehat{BAC}\) (3)
Theo cmt, AO là trung trực BC, mà I thuộc AO \(\Rightarrow IB=IC\)
\(\Rightarrow\Delta IBC\) cân tại I \(\Rightarrow\widehat{IBC}=\widehat{ICB}\)
Lại có \(\widehat{ICB}=\widehat{ABI}\) (cùng chắn BI)
\(\Rightarrow\widehat{IBC}=\widehat{ABI}\)
\(\Rightarrow BI\) là tia phân giác của \(\widehat{ABC}\) (4)
(3);(4) \(\Rightarrow I\) là giao điểm 2 đường phân giác trong tam giác ABC nên I là tâm đường tròn nội tiếp tam giác ABC
V.
\(\left\{{}\begin{matrix}x^2+3y-6x=0\\9x^2-6xy^2+y^4-3y+9=0\end{matrix}\right.\)
Cộng vế với vế:
\(\Rightarrow9x^2-6xy^2+y^4+x^2-6x+9=0\)
\(\Leftrightarrow\left(3x-y^2\right)^2+\left(x-3\right)^2=0\)
Mà \(\left\{{}\begin{matrix}\left(3x-y^2\right)^2\ge0\\\left(x-3\right)^2\ge0\end{matrix}\right.\) ; \(\forall x;y\)
Nên đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}3x-y^2=0\\x-3=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y^2=3x\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y^2=9\\x=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\\x=3\end{matrix}\right.\)
Thế vào pt \(x^2+3y-6x=0\) thấy chỉ có \(\left\{{}\begin{matrix}x=3\\y=3\end{matrix}\right.\) thỏa mãn
Vậy hệ có nghiệm duy nhất \(\left(x;y\right)=\left(3;3\right)\)
II.2
Gọi bán kính đáy của hình trụ là R (cm) với R>0
Chiều cao hình trụ là: \(h=2R\) (cm)
Diện tích toàn phần của hình trụ là:
\(2\pi R^2+2\pi R.h=6\pi R^2\)
Do diện tích toàn phần là \(48\pi\left(cm^2\right)\) nên ta có pt:
\(6\pi R^2=48\pi\Rightarrow R=2\sqrt{2}\left(cm\right)\)
Chiều cao trụ là: \(h=2R=4\sqrt{2}\left(cm\right)\)
Thể tích trụ là:
\(V=\pi R^2.h=\pi.\left(2\sqrt{2}\right)^2.4\sqrt{2}=32\pi\sqrt{2}\left(cm^3\right)\)
III.2
a.
Ta có: \(\Delta=\left(-3\right)^2-4\left(-m^2+1\right)=4m^2+5>0;\forall m\)
\(\Rightarrow\) Pt luôn có 2 nghiệm pb với mọi m
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=-m^2+1\end{matrix}\right.\)
Áp dụng BĐT trị tuyệt đối ta có:
\(\left|x_1\right|+2\left|x_2\right|=\left|x_1\right|+\left|x_2\right|+\left|x_2\right|\ge\left|x_1+x_2\right|+\left|x_2\right|=3+\left|x_2\right|\)
Mà \(\left|x_1\right|+2\left|x_2\right|=3\)
\(\Rightarrow3\ge3+\left|x_2\right|\Rightarrow\left|x_2\right|\le0\)
\(\Rightarrow\left|x_2\right|=0\Rightarrow x_2=0\)
Thế vào \(x_1x_2=-m^2+1\Rightarrow-m^2+1=0\)
\(\Rightarrow m=\pm1\)




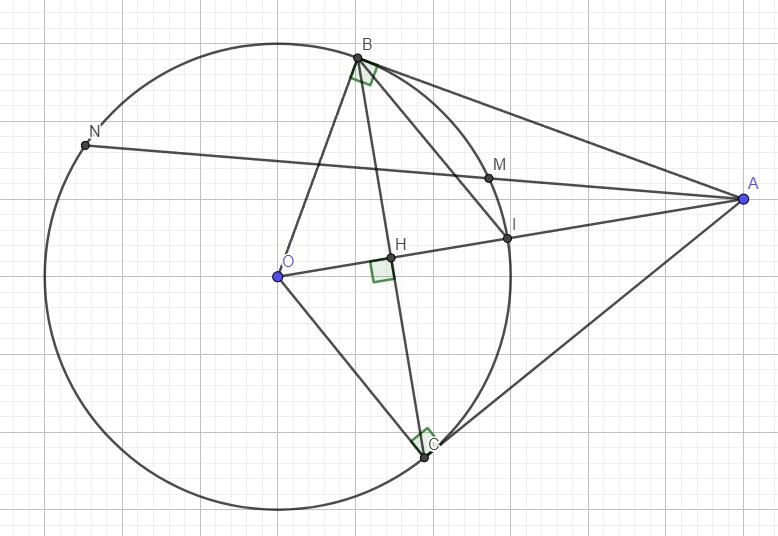













 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ