mấy chỗ này rút gọn đi thôi
a) \(\frac{-4xy^2}{2x^4y}=\frac{2y}{-x^3}\)
Biến đổi vế trái ta có:
\(\frac{-4xy^2}{2x^4y}=\frac{-2y}{x^3}=\frac{2y}{-x^3}\)
=> 2y/-x^3=2y/-x^3
Nên \(\frac{-4xy^2}{2x^4y}=\frac{2y}{-x^3}\) ( đpcm)
b) \(\frac{m^2-2mn+n^2}{m^2-n^2}=\frac{m-n}{m+n}\)
Biến đổi vế trái ta có:
\(\frac{m^2-2mn+n^2}{m^2-n^2}=\frac{\left(m-n\right)^2}{\left(m-n\right)\left(m+n\right)}=\frac{m-n}{m+n}\)
=> VT=VP=\(\frac{m-n}{m+n}\) (đpcm)
c)\(\frac{a-b}{11}=\frac{3a\left(a-b\right)^2}{33a^2-33ab}\)
BĐ VP ta có:
\(\frac{3a\left(a-b\right)^2}{33a^2-33ab}=\frac{3a\left(a-b\right)^2}{33a\left(a-b\right)}=\frac{a-b}{11}\)
=> VT=VP=\(\frac{a-b}{11}\)(đpcm)
d) \(\frac{a^2+4ab+4b^2}{a^2-4b}=\frac{a+2b}{a-2b}\)
Bđ VT ta có:
\(\frac{a^2+4ab+4b^2}{a^2-4b}=\frac{\left(a+2b\right)^2}{\left(a-2b\right)\left(a+2b\right)}=\frac{a+2b}{a-2b}\)
=> VT=VP=\(\frac{a+2b}{a-2b}\)(đpcm)







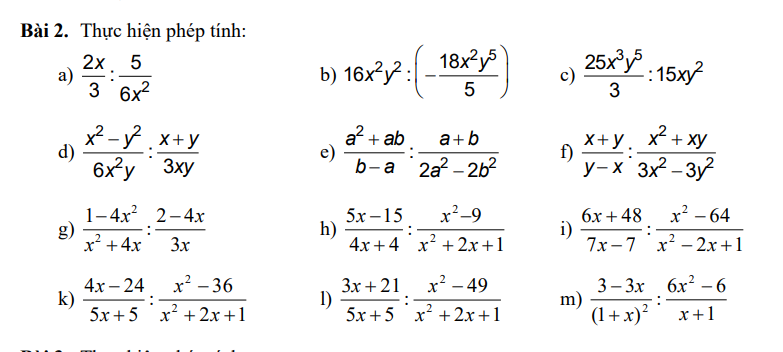



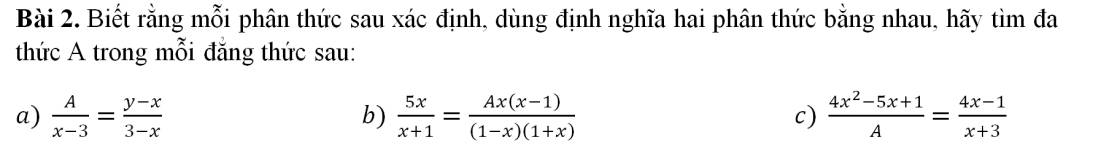 giúp em bài này với ạ ! Em cảm ơn ạ
giúp em bài này với ạ ! Em cảm ơn ạ 

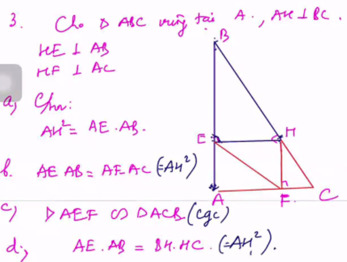



 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ