Bài 3.37
a) Do BE // AC (gt)
⇒ ∠ABE = ∠A = 80⁰ (so le trong)
Do CF // AB
⇒ ∠ACF = ∠A = 80⁰ (so le trong)
⇒ ∠ABE = ∠ACF = 80⁰
b) Do CF // AB
⇒ ∠FCz = ∠ABC = 60⁰ (đồng vị)
Ta có:
∠BCF + ∠FCz = 180⁰ (kề bù)
⇒ ∠BCF = 180⁰ - ∠FCz
= 180⁰ - 60⁰
= 120⁰
⇒ ∠ACB = ∠BCF - ∠ACF
= 120⁰ - 80⁰
= 40⁰
c) Do Bx là tia phân giác của ∠ABE
⇒ ∠ABx = ∠ABE : 2 = 80⁰ : 2 = 40⁰
⇒ ∠xBC = ∠ABx + ∠ABC
= 40⁰ + 60⁰
= 100⁰
Do Cy là tia phân giác của ∠ACF
⇒ ∠yCF = ∠ACF : 2 = 80⁰ : 2 = 40⁰
⇒ ∠yCz = ∠yCF + ∠FCz
= 40⁰ + 60⁰
= 100⁰
⇒ ∠xBC = ∠yCz = 100⁰
Mà ∠xBC và ∠yCz là hai góc đồng vị
⇒ Bx // Cy
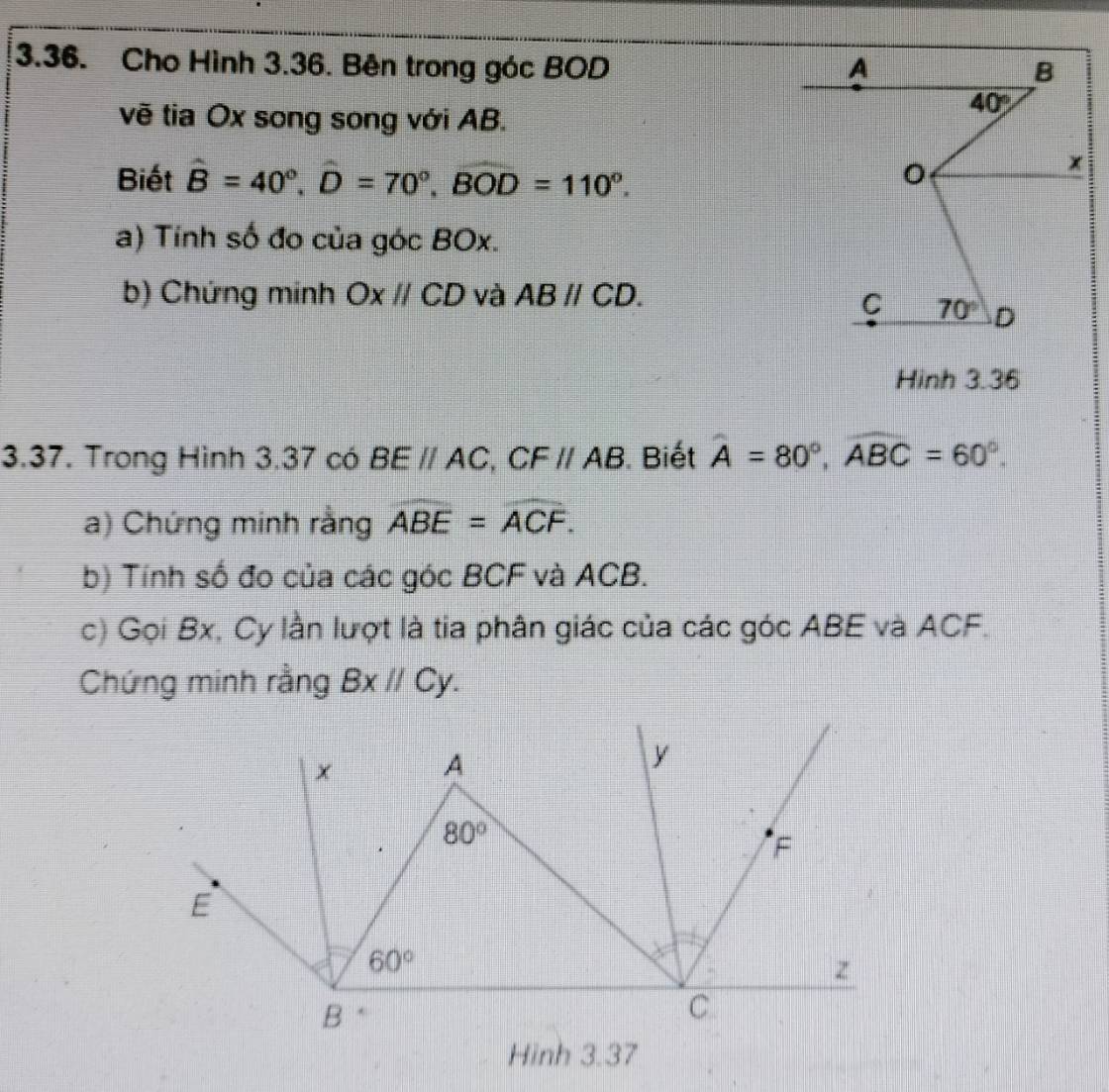
Bài 3.36
a) Do Ox // AB
⇒ ∠BOx = ∠ABO = 40⁰ (so le trong)
b) Ta có:
∠xOD = ∠BOD - ∠BOx
= 110⁰ - 40⁰
= 70⁰
⇒ ∠xOD = ∠ODC = 70⁰
Mà ∠xOD và ∠ODC là hai góc so le trong
⇒ Ox // CD
Mà Ox // AB (gt)
⇒ AB // CD

 giup em dc ko a em dang can gap a ko can ve hinh dau a
giup em dc ko a em dang can gap a ko can ve hinh dau a


 giup em voi mn ko can ve hinh dau de em tu ve cung dc a
giup em voi mn ko can ve hinh dau de em tu ve cung dc a






