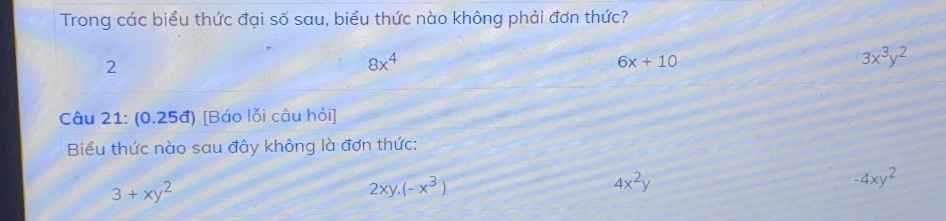
a: Ta có: \(\widehat{BAK}+\widehat{BAC}=\widehat{KAC}=90^0\)
\(\widehat{EAC}+\widehat{BAC}=\widehat{BAE}=90^0\)
Do đó: \(\widehat{BAK}=\widehat{EAC}\)
Xét ΔBAK và ΔEAC có
BA=EA
\(\widehat{BAK}=\widehat{EAC}\)
AK=AC
Do đó: ΔBAK=ΔEAC
=>BK=EC
b: Xét ΔDBN và ΔDCA có
DB=DC
\(\widehat{BDN}=\widehat{CDA}\)(hai góc đối đỉnh)
DN=DA
Do đó: ΔDBN=ΔDCA
=>BN=CA
=>BN=AK
Xét ΔDBA và ΔDCN có
DB=DC
\(\widehat{BDA}=\widehat{CDN}\)(hai góc đối đỉnh)
DA=DN
Do đó: ΔDBA=ΔDCN
=>BA=CN
=>CN=AE
Xét ΔAKE và ΔCAN có
AK=CA
\(\widehat{KAE}=\widehat{ACN}\)
AE=CN
Do đó: ΔAKE=ΔCAN
Đúng 1
Bình luận (0)
ai giúp em làm câu này vs em đang cần gấp ạ
