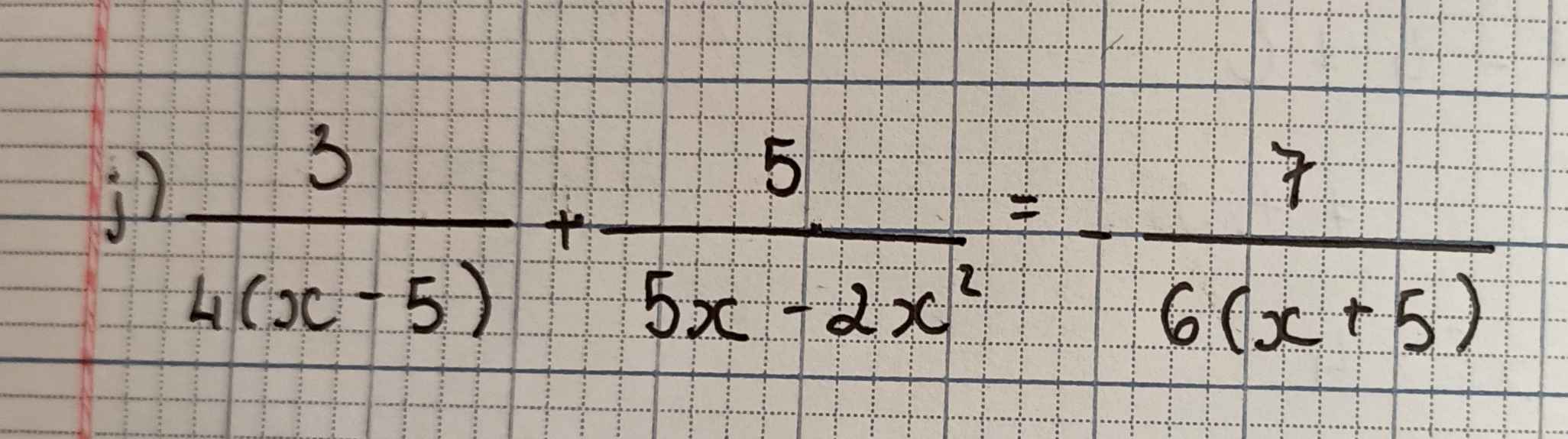ĐKXĐ: \(x\notin\left\{5;-5;0;\dfrac{5}{2}\right\}\)
\(\dfrac{3}{4\left(x-5\right)}+\dfrac{5}{5x-2x^2}=\dfrac{-7}{6\left(x+5\right)}\)
=>\(\dfrac{3}{4\left(x-5\right)}+\dfrac{7}{6\left(x+5\right)}=\dfrac{-5}{5x-2x^2}\)
=>\(\dfrac{9\left(x+5\right)+14\left(x-5\right)}{12\left(x-5\right)\left(x+5\right)}=\dfrac{5}{x\left(2x-5\right)}\)
=>\(\dfrac{23x-25}{12\left(x-5\right)\left(x+5\right)}=\dfrac{5}{x\left(2x-5\right)}\)
=>\(60\left(x-5\right)\left(x+5\right)=\left(2x^2-5x\right)\left(23x-25\right)\)
=>\(46x^3-50x^2-115x^2+125x=60\left(x^2-25\right)\)
=>\(46x^3-165x^2+125x-60x^2+1500=0\)
=>\(46x^3-225x^2+125x+1500=0\)
=>\(x\simeq-1,99\left(nhận\right)\)