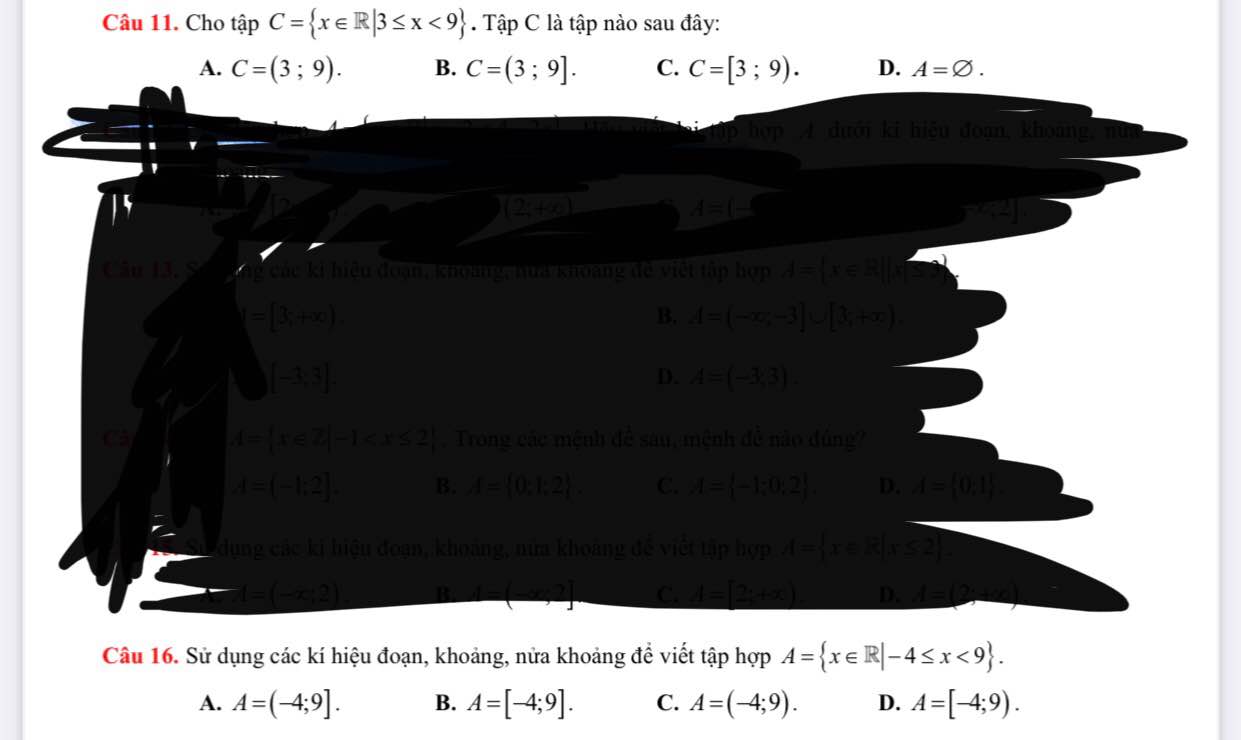Phương trình hoành độ giao điểm là:
\(-2x^2+3x+1=mx-2m+1\)
\(\Leftrightarrow-2x^2+\left(3-m\right)x+2m=0\)
Để (P) tiếp xúc với (d) thì \(\left(3-m\right)^2-4\cdot\left(-2\right)\cdot2m=0\)
\(\Leftrightarrow m^2-6m+9+16m=0\)
\(\Leftrightarrow m^2-25m+9=0\)(1)
\(\text{Δ}=\left(-25\right)^2-4\cdot9=625-36=589\)
Vì Δ>0 nên phương trình (1) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{25-\sqrt{589}}{2}\\m_2=\dfrac{25+\sqrt{589}}{2}\end{matrix}\right.\)








 giúp em mấy câu này với ạ
giúp em mấy câu này với ạ