a: Thay x=25 vào A, ta được:
\(A=\dfrac{25-10}{5}=\dfrac{15}{5}=3\)
b: \(B=\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{2-\sqrt{x}}+\dfrac{x-2\sqrt{x}+4}{x-4}\)
\(=\dfrac{1}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}-2}+\dfrac{x-2\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2-\sqrt{x}-2+x-2\sqrt{x}+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-2\sqrt{x}}{\left(\sqrt{x}+2\right)\cdot\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
c: \(P=A\cdot B=\dfrac{\sqrt{x}}{\sqrt{x}+2}\cdot\dfrac{x-10}{\sqrt{x}}=\dfrac{x-10}{\sqrt{x}+2}\)
P<1
=>P-1<0
=>\(\dfrac{x-10-\sqrt{x}-2}{\sqrt{x}+2}< 0\)
=>\(x-\sqrt{x}-12< 0\)
=>\(\left(\sqrt{x}-4\right)\left(\sqrt{x}+3\right)< 0\)
=>\(\sqrt{x}-4< 0\)
=>\(\sqrt{x}< 4\)
=>0<=x<16
mà x là số nguyên tố lớn nhất
nên x=13
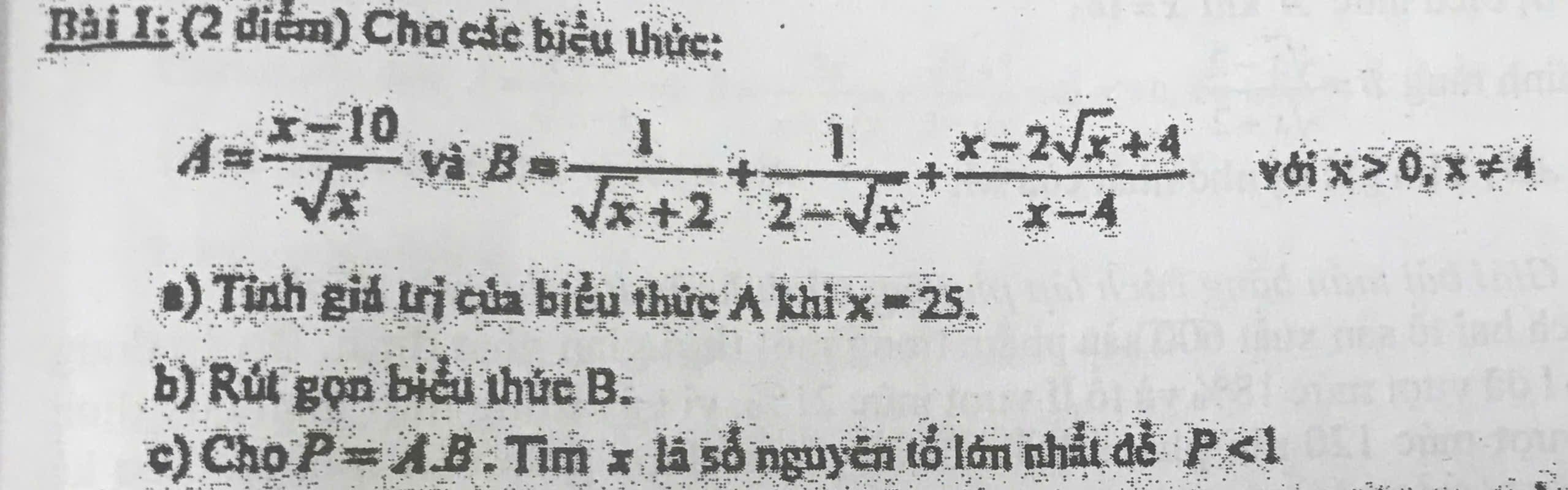
Mn giup em cau nay a!
