\(A=\left(\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\left(\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right).\left(\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b.
\(x=\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}=\sqrt{\left(\sqrt{2}+1\right)^2}-\sqrt{\left(\sqrt{2}-1\right)^2}\)
\(=\left|\sqrt{2}+1\right|-\left|\sqrt{2}-1\right|=\sqrt{2}+1-\sqrt{2}+1=2\)
\(\Rightarrow A=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}=\dfrac{\left(\sqrt{2}+1\right)^2}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}=\dfrac{3+2\sqrt{2}}{1}=3+2\sqrt{2}\)
c.
\(A=\sqrt{x}\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\sqrt{x}\)
\(\Rightarrow\sqrt{x}+1=x-\sqrt{x}\Rightarrow x-2\sqrt{x}-1=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=1+\sqrt{2}\\\sqrt{x}=1-\sqrt{2}< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\left(1+\sqrt{2}\right)^2=3+2\sqrt{2}\)
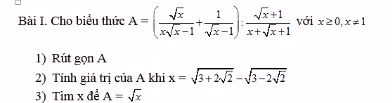
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
