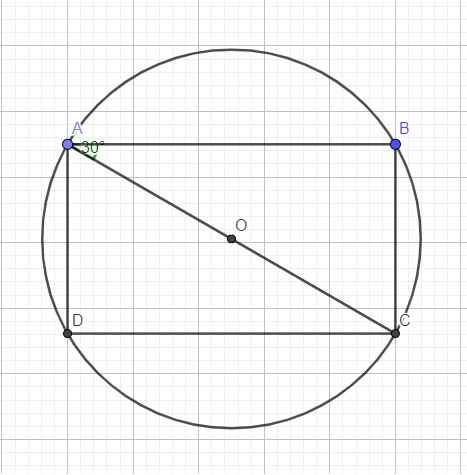
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{ABC}=90^0\Rightarrow\) B là góc nội tiếp chắn nửa đường tròn hay AC là đường kính
\(\Rightarrow AC=2R=100\left(cm\right)\)
Trong tam giác vuông ABC ta có:
\(sin\widehat{BAC}=\dfrac{BC}{AC}\Rightarrow BC=AC.sin\widehat{BAC}=100.sin30^0=50\left(cm\right)\)
\(\Rightarrow AD=BC=50\left(cm\right)\)
Áp dụng định lý Pitago:
\(AB=\sqrt{AC^2-BC^2}=50\sqrt{3}\left(cm\right)=CD\)
Đúng 0
Bình luận (1)