giúp e vs, vẽ hình giúp e vs ạ
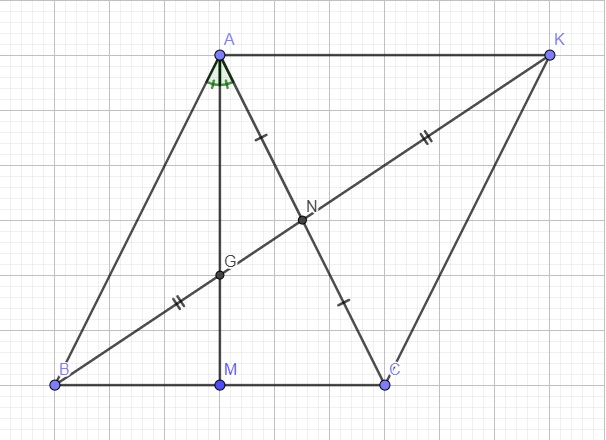
a.
Do AM là phân giác \(\Rightarrow\widehat{BAM}=\widehat{CAM}\)
Xét hai tam giác BAM và CAM có:
\(\left\{{}\begin{matrix}AB=AC\left(\Delta ABC\text{ cân}\right)\\\widehat{BAM}=\widehat{CAM}\\AM\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta BAM=\Delta CAM\left(c.g.c\right)\Rightarrow BM=CM\)
\(\Rightarrow M\) là trung điểm BC
\(\Rightarrow AM\) là trung tuyến
b.
Do \(NB=NK\Rightarrow N\) là trung điểm BK
Lại có N là trung điểm AC
\(\Rightarrow\) AC và BK cắt nhau tại trung điểm mỗi đường
\(\Rightarrow ABCK\) là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)
\(\Rightarrow AB||CK\) và \(AB=CK\)
c.
N là trung điểm AC \(\Rightarrow BN\) là 1 trung tuyến của tam giác ABC
Lại có AM cũng là trung tuyến
\(\Rightarrow G\) là giao điểm 2 đường trung tuyến
\(\Rightarrow\) G là trọng tâm tam giác ABC
\(\Rightarrow BG=\dfrac{2}{3}BN\) (t/c trọng tâm)
Mà \(BN=NK\left(gt\right)\Rightarrow BN=\dfrac{1}{2}BK\)
\(\Rightarrow BG=\dfrac{2}{3}.\dfrac{1}{2}BK=\dfrac{1}{3}BK\)
\(\Rightarrow BK=3BG\)
