a) |2x + 7| = 3x + 5 (1)
|2x + 7| = 2x + 7 ⇔2x + 7 ≥ 0 ⇔ 2x ≥ -7 ⇔ x ≥ -7/2
|2x + 7| = -2x - 7 ⇔ 2x + 7 < 0 ⇔ 2x < -7 ⇔ x < -7/2
*) Với x ≥ -7/2
(1) ⇔ 2x + 7 = 3x + 5
⇔ 2x - 3x = 5 - 7
⇔ -x = -2
⇔ x = 2 (nhận)
*) Với x < -7/2
(1) ⇔ -2x - 7 = 3x + 5
⇔ -2x - 3x = 5 + 7
⇔ -5x = 12
⇔ x = -12/5 (loại)
Vậy S = {2}
b) (3x + 5)/6 = (1 - 2x)/4
⇔ 2(3x + 5) = 3(1 - 2x)
⇔ 6x + 10 = 3 - 6x
⇔ 6x + 6x = 3 - 10
⇔ 12x = -7
⇔ x = -7/12
Vậy S = {-7/12}
c) (x + 1)/(x - 2) - (x - 3)/(x + 2) - (x² + 16)/(4 - x²) = 0
⇔ (x + 1)/(x - 2) - (x - 3)(x + 2) + (x² - 16)/(x² - 4) = 0 (1)
ĐKXĐ: x ≠ 2; x ≠ -2
(1) ⇔ (x + 1)(x + 2) - (x - 3)(x - 2) + (x² - 16) = 0
⇔ x² + 2x + x + 2 - x² + 2x + 3x - 6 + x² - 16 = 0
⇔ x² + 8x - 20 = 0
⇔ x² - 10x + 2x - 20 = 0
⇔ (x² - 10x) + (2x - 20) = 0
⇔ x(x - 10) + 2(x - 10) = 0
⇔ (x - 10)(x + 2) = 0
⇔ x - 10 = 0 hoặc x + 2 = 0
*) x - 10 = 0
⇔ x = 10 (nhận)
*) x + 2 = 0
⇔ x = -2 (loại)
Vậy S = {-2}

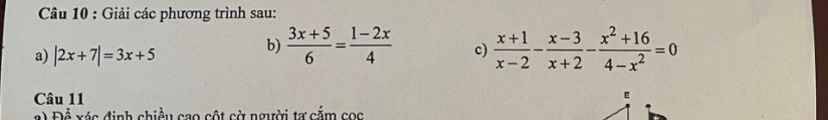










 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ


