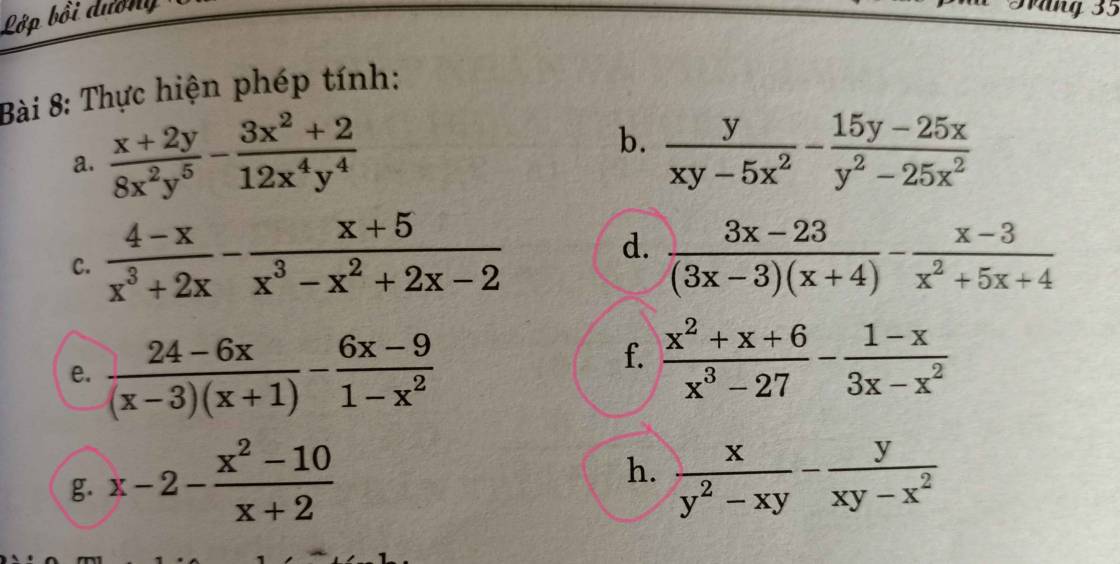d: ĐKXĐ: \(x\notin\left\{1;-4;-1\right\}\)
\(\dfrac{3x-23}{\left(3x-3\right)\left(x+4\right)}-\dfrac{x-3}{x^2+5x+4}\)
\(=\dfrac{3x-23}{3\cdot\left(x-1\right)\left(x+4\right)}-\dfrac{x-3}{\left(x+1\right)\left(x+4\right)}\)
\(=\dfrac{\left(3x-23\right)\left(x+1\right)-3\left(x-3\right)\left(x-1\right)}{3\left(x-1\right)\left(x+1\right)\left(x+4\right)}\)
\(=\dfrac{3x^2+3x-23x-23-3\left(x^2-4x+3\right)}{3\left(x-1\right)\left(x+1\right)\left(x+4\right)}\)
\(=\dfrac{3x^2-20x-23-3x^2+12x-9}{3\left(x-1\right)\left(x+1\right)\left(x+4\right)}\)
\(=\dfrac{-8x-32}{3\left(x-1\right)\left(x+1\right)\left(x+4\right)}=\dfrac{-8}{3\left(x-1\right)\left(x+1\right)}\)
e: ĐKXĐ: \(x\notin\left\{3;-1;1\right\}\)
\(\dfrac{24-6x}{\left(x-3\right)\left(x+1\right)}-\dfrac{6x-9}{1-x^2}\)
\(=\dfrac{24-6x}{\left(x-3\right)\left(x+1\right)}+\dfrac{6x-9}{\left(x-1\right)\cdot\left(x+1\right)}\)
\(=\dfrac{\left(24-6x\right)\left(x-1\right)+\left(6x-9\right)\left(x-3\right)}{\left(x-3\right)\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{24x-24-6x^2+6x+6x^2-18x-9x+27}{\left(x-3\right)\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{3x+3}{\left(x-3\right)\left(x+1\right)\left(x-1\right)}=\dfrac{3}{\left(x-1\right)\left(x-3\right)}\)
f: ĐKXĐ: \(x\notin\left\{0;3\right\}\)
\(\dfrac{x^2+x+6}{x^3-27}-\dfrac{1-x}{3x-x^2}\)
\(=\dfrac{x^2+x+6}{\left(x-3\right)\left(x^2+3x+9\right)}-\dfrac{x-1}{x\left(x-3\right)}\)
\(=\dfrac{x\left(x^2+x+6\right)-\left(x-1\right)\left(x^2+3x+9\right)}{x\left(x-3\right)\left(x^2+3x+9\right)}\)
\(=\dfrac{x^3+x^2+6x-x^3-3x^2-9x+x^2+3x+9}{x\left(x-3\right)\left(x^2+3x+9\right)}\)
\(=\dfrac{-x^2+9}{x\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{-x-3}{x\left(x^2+3x+9\right)}\)
g: ĐKXĐ: x<>-2
\(x-2-\dfrac{x^2-10}{x+2}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)-x^2+10}{x+2}\)
\(=\dfrac{x^2-4-x^2+10}{x+2}=\dfrac{6}{x+2}\)
h: \(\dfrac{x}{y^2-xy}-\dfrac{y}{xy-x^2}\)
\(=\dfrac{x}{y\left(y-x\right)}-\dfrac{y}{x\left(y-x\right)}\)
\(=\dfrac{x^2-y^2}{xy\left(y-x\right)}=\dfrac{-x-y}{xy}\)