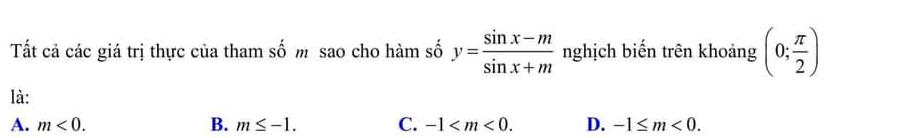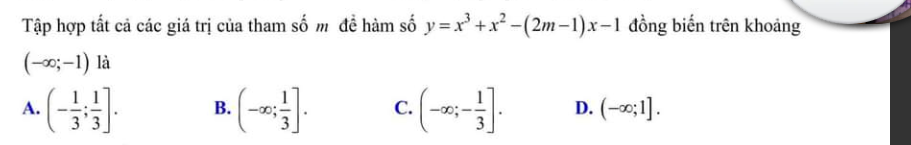\(y=x^3+x^2-\left(2m-1\right)x-1\)
\(\Rightarrow y'=3x^2+2x-\left(2m-1\right)=3x^2+2x+1-2m\)
HSĐB trên \(\left(-\infty;-1\right)\) \(\Leftrightarrow y'\ge0\forall x\in\left(-\infty;-1\right)\)
\(\Leftrightarrow m\le\dfrac{3x^2+2x+1}{2}=g\left(x\right)\forall x\in\left(-\infty;-1\right)\)
Tức là : m \(\le Ming\left(x\right)\forall x\in\left(-\infty;-1\right)\)
g'(x) = \(\dfrac{6x+2}{2}=3x+1\) ; g'(x) = 0 \(\Leftrightarrow x=-\dfrac{1}{3}\)
Lập bảng BBT ; nhìn vào BBT ; ta thấy Min g(x) trên \(\left(-\infty;-1\right)=\dfrac{1}{3}\) tại x = -1/3 . Suy ra : \(m\le\dfrac{1}{3}\)
Chọn B
P/s : Câu 1 mik chưa làm chắc làm giống câu 2