1) -Áp dụng đ/l phân giác ngoài của tam giác là ra, còn nếu đề bắt c/m định lí đó thì mình sẽ c/m.
-CF//AB (F thuộc AE).
-Dễ dàng c/m: \(\widehat{CAF}=\widehat{CFA}\) (cùng bằng \(\widehat{BAE}\))
\(\Rightarrow\)△ACF cân tại C \(\Rightarrow AC=CF\).
-△CEF có: AB//CF \(\Rightarrow\dfrac{BE}{CE}=\dfrac{AB}{CF}=\dfrac{AB}{AC}\)
2) -Ta có: \(\widehat{BAC}\) và \(\widehat{BAx}\) (tia Ax là tia đối của tia AB) là 2 góc kề bù.
\(\Rightarrow\widehat{DAE}=90^0\) (định lí về góc tạo bởi 2 tia p/g của 2 góc kề bù).
\(\Rightarrow\)△ADE vuông tại A.
3) -Giả sử AB>AC.
-△ABC có: AD, AE là p/g trong và ngoài.
\(\Rightarrow\dfrac{BD}{CD}=\dfrac{BE}{CE}=\dfrac{AB}{AC}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{BD+CD}{AB+AC}=\dfrac{BC}{AB+AC}\Rightarrow BD=\dfrac{AB.BC}{AB+AC}\\\dfrac{BE}{AB}=\dfrac{CE}{AC}=\dfrac{BE-CE}{AB-AC}=\dfrac{BC}{AB-AC}\Rightarrow BE=\dfrac{AB.BC}{AB-AC}\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{BD}+\dfrac{1}{BE}=\dfrac{AB+AC}{AB.BC}+\dfrac{AB-AC}{AB.BC}=\dfrac{2AB}{AB.BC}=\dfrac{2}{BC}\)





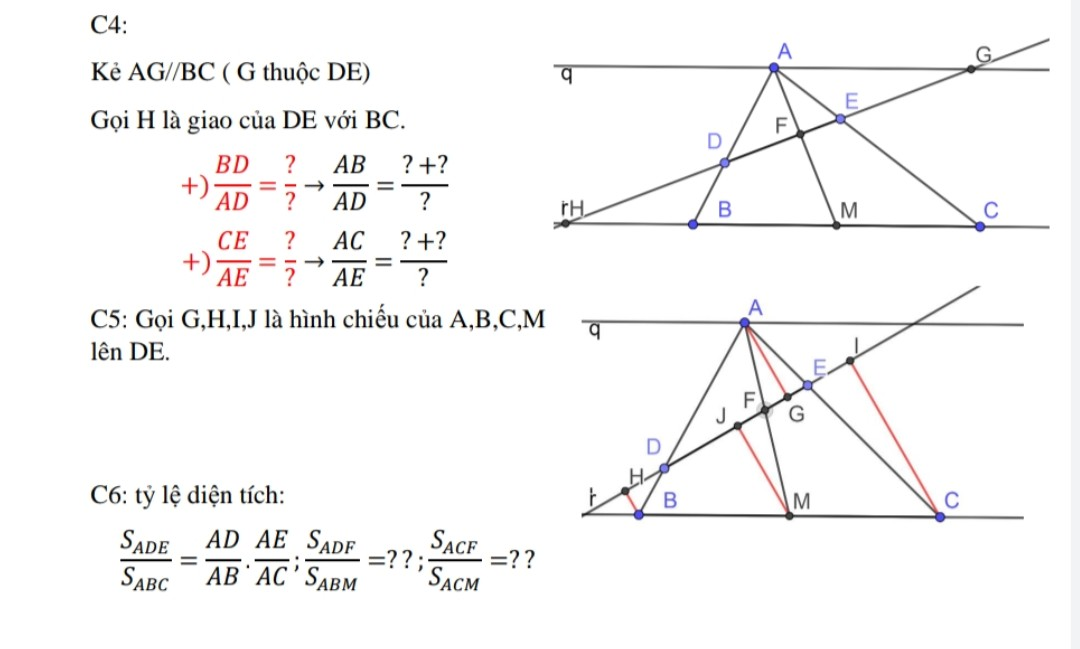 huhu giúp e với ạ
huhu giúp e với ạ


