1: \(P=\dfrac{x-4-x+2\sqrt{x}+3-3\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{-1}{\sqrt{x}-3}\)
2: Để P<-1 thì P+1<0
\(\Leftrightarrow\dfrac{-1+\sqrt{x}-3}{\sqrt{x}-3}< 0\)
=>\(3< \sqrt{x}< 4\)
=>9<x<16
\(3;\) \(x\in Z;P\in Z?\)
\(\Rightarrow\dfrac{-1}{\sqrt{x}-3}\in Z\Leftrightarrow\sqrt{x}-3\inƯ\left(1\right)=\left(\pm1\right)\Leftrightarrow x=\left\{16;4\right\}\)
\(đkxđ:x\ge0;x\ne9;x\ne4\Rightarrow x=16\left(tm\right)\)

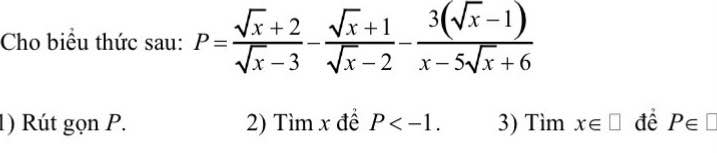

















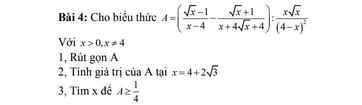 Mn giúp e với
Mn giúp e với