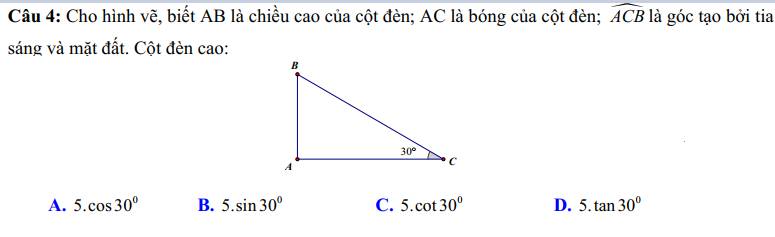
1) \(\dfrac{4\sqrt{x}-x-4}{x-4}\)
\(=\dfrac{-x+4\sqrt{x}-4}{x-4}\)
\(=\dfrac{-\left(x-4\sqrt{x}+4\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+2}\)
\(=\dfrac{-\sqrt{x}+2}{\sqrt{x}+2}\)
2) \(\dfrac{x+y-2\sqrt{xy}}{x\sqrt{y}-y\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}\)
\(=\dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{xy}}\)
3) \(\dfrac{x-9}{x\sqrt{x}-27}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}\right)^3-3^3}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(x+3\sqrt{x}+9\right)}\)
\(=\dfrac{\sqrt{x}+3}{x+3\sqrt{x}+9}\)
\(1,\dfrac{4\sqrt{x}-x-4}{x-4}\left(dk:x\ge0,x\ne4\right)\\ =\dfrac{-\left(x-4\sqrt{x}+4\right)}{\sqrt{x^2}-2^2}=\dfrac{-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+2}=\dfrac{2-\sqrt{x}}{\sqrt{x}+2}\)
\(2,\dfrac{x+y-2\sqrt{xy}}{x\sqrt{y}-y\sqrt{x}}\left(dk:x,y\ge0\right)\\ =\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}=\dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{xy}}\)
\(3,\dfrac{x-9}{x\sqrt{x}-27}\left(dk:x\ge0\right)\\ =\dfrac{\sqrt{x^2}-3^2}{\sqrt{x^3}-3^3}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(x+3\sqrt{x}+9\right)}=\dfrac{\sqrt{x}+3}{x+3\sqrt{x}+9}\)
1) \(\dfrac{4\sqrt{x}-x-4}{x-4}=\dfrac{-\left(x-4\sqrt{x}+4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+2}\)
2) \(\dfrac{x+y-2\sqrt{xy}}{x\sqrt{y}-y\sqrt{x}}=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}=\dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{xy}}\)
3) \(\dfrac{x-9}{x\sqrt{x}-27}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}\right)^3-3^3}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(x+3\sqrt{x}+9\right)}=\dfrac{\sqrt{x}+3}{x+3\sqrt{x}+9}\)

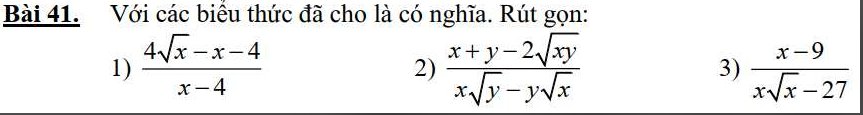 giúp e gấp với ạ, e cảm ơn
giúp e gấp với ạ, e cảm ơn














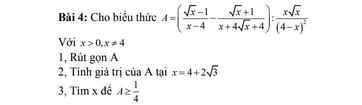 Mn giúp e với
Mn giúp e với