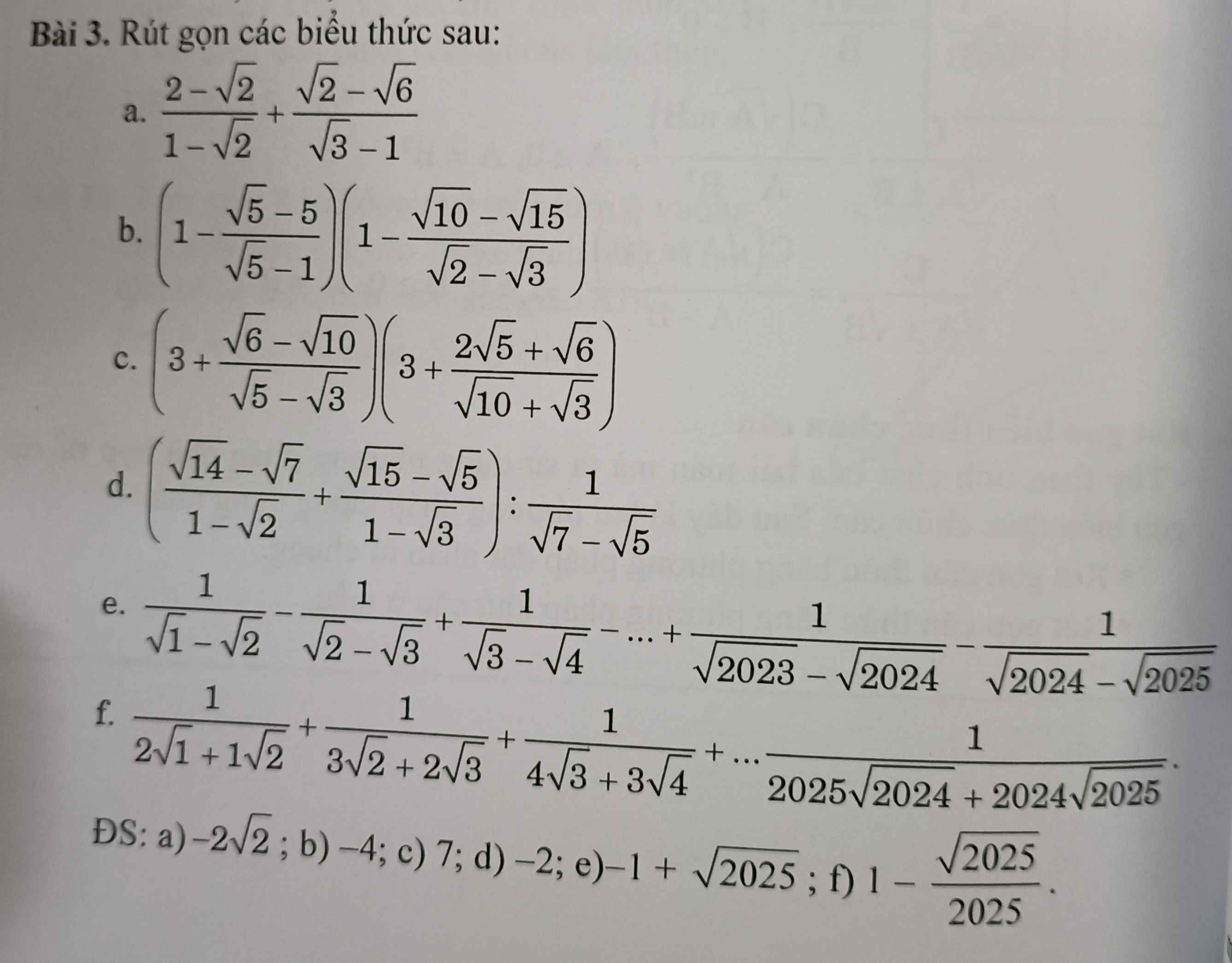c: \(\left(3+\dfrac{\sqrt{6}-\sqrt{10}}{\sqrt{5}-\sqrt{3}}\right)\left(3+\dfrac{2\sqrt{5}+\sqrt{6}}{\sqrt{10}+\sqrt{3}}\right)\)
\(=\left[3+\dfrac{\sqrt{2}\left(\sqrt{3}-\sqrt{5}\right)}{-\left(\sqrt{3}-\sqrt{5}\right)}\right]\cdot\left[3+\dfrac{\sqrt{2}\left(\sqrt{10}+\sqrt{3}\right)}{\sqrt{10}+\sqrt{3}}\right]\)
\(=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)=9-2=7\)
d: \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{-\left(\sqrt{3}-1\right)}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)\)
\(=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
\(=-\left(7-5\right)=-2\)