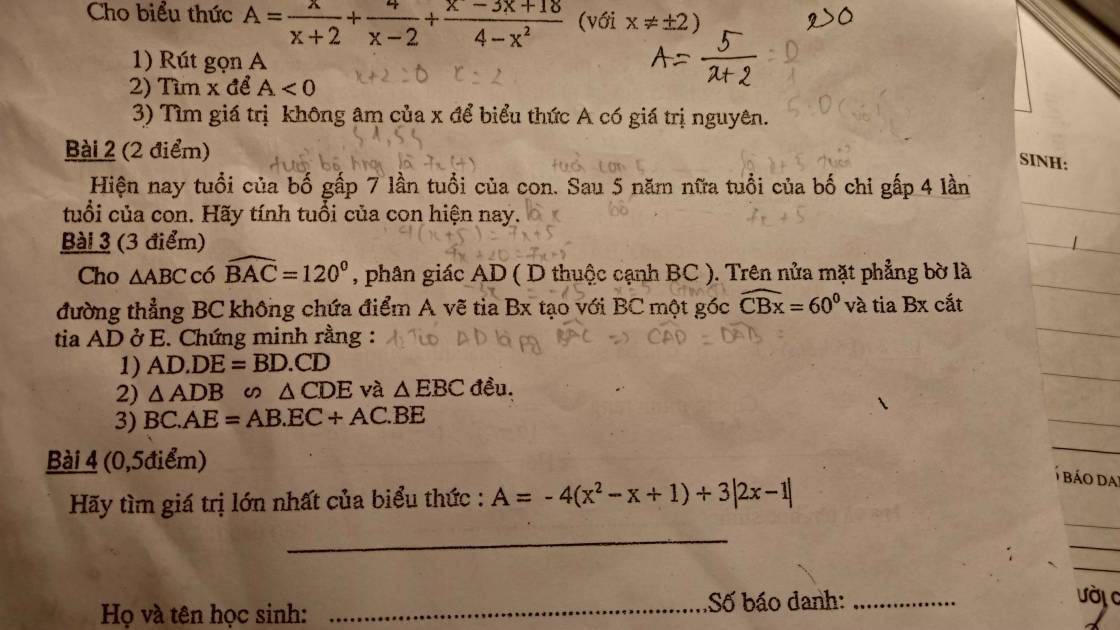Bài 3:
1: AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{BAC}}{2}=60^0\)
Xét ΔDAC và ΔDBE có
\(\widehat{DAC}=\widehat{DBE}\left(=60^0\right)\)
\(\widehat{ADC}=\widehat{BDE}\)(hai góc đối đỉnh)
Do đó: ΔDAC~ΔDBE
=>\(\dfrac{DA}{DB}=\dfrac{DC}{DE}\)
=>\(\dfrac{DA}{DC}=\dfrac{DB}{DE}\)
=>\(DA\cdot DE=DB\cdot DC\)
2: Xét ΔDAB và ΔDCE có
\(\dfrac{DA}{DC}=\dfrac{DB}{DE}\)
\(\widehat{ADB}=\widehat{CDE}\)(hai góc đối đỉnh)
Do đó: ΔDAB~ΔDCE
=>\(\widehat{DAB}=\widehat{DCE}=60^0\)
Xét ΔECB có \(\widehat{ECB}=\widehat{EBC}\left(=60^0\right)\)
nên ΔECB đều
Đúng 1
Bình luận (0)
