Câu 7:
\(A=4+4^2+4^3+...+4^{2003}+4^{2004}\)
=>\(4\cdot A=4^2+4^3+4^4+...+4^{2004}+4^{2005}\)
=>\(4\cdot A-A=4^2+4^3+4^4+...+4^{2004}+4^{2005}-4-4^2-...-4^{2003}-4^{2004}\)
=>\(3\cdot A=4^{2005}-4\)
=>\(3\cdot A+4=4^{2005}=4^{2004}\cdot4⋮4^{2004}\)
Bài 8:
\(A=5+4^2+4^3+...+4^{2020}+4^{2021}\)
=>\(A=1+4+4^2+4^3+...+4^{2020}+4^{2021}\)
=>\(4\cdot A=4+4^2+4^3+4^4+...+4^{2021}+4^{2022}\)
=>\(4\cdot A-A=4+4^2+4^3+...+4^{2021}+4^{2022}-1-4-4^2-...-4^{2020}-4^{2021}\)
=>\(3\cdot A=4^{2022}-1\)
=>\(3\cdot A+1=4^{2022}=4^{2021}\cdot4⋮4^{2021}\)

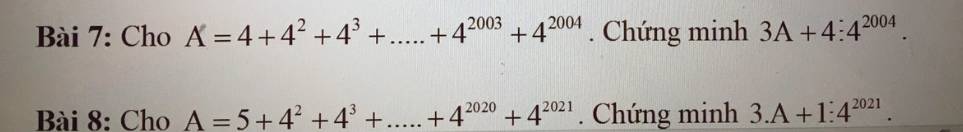




 giải hộ mình bài 5 với ạaaa
giải hộ mình bài 5 với ạaaa








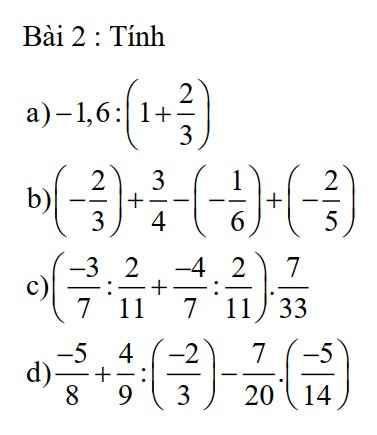 giúp với giúp với giúp e với ạ. e cảm ơn
giúp với giúp với giúp e với ạ. e cảm ơn