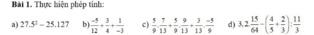e/\(E=\dfrac{7}{3}+\dfrac{7}{15}+\dfrac{7}{35}+...+\dfrac{7}{575}\)
\(=\dfrac{7}{1.3}+\dfrac{7}{3.5}+\dfrac{7}{5.7}+...+\dfrac{7}{23.25}\)
\(=\dfrac{7}{2}\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{23.25}\right)\)
\(=\dfrac{7}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{23}-\dfrac{1}{25}\right)\)
\(=\dfrac{7}{2}\left(1-\dfrac{1}{25}\right)\)
\(=\dfrac{7}{2}\cdot\dfrac{24}{25}\)
\(=\dfrac{84}{25}\)
g)\(G=\dfrac{5}{2.4}+\dfrac{5}{4.6}+\dfrac{5}{6.8}+...+\dfrac{5}{100.102}\)
\(=\dfrac{5}{2}\left(\dfrac{2}{2.4}+\dfrac{2}{4.6}+\dfrac{2}{6.8}+...+\dfrac{2}{100.102}\right)\)
\(=\dfrac{5}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{8}+...+\dfrac{1}{100}-\dfrac{1}{102}\right)\)
\(=\dfrac{5}{2}\left(\dfrac{1}{2}-\dfrac{1}{102}\right)\)
\(=\dfrac{5}{2}\cdot\dfrac{25}{51}\)
\(=\dfrac{125}{102}\)
h/\(H=\dfrac{2024}{2.5}+\dfrac{2024}{5.8}+...+\dfrac{2024}{62.65}\)
\(=\dfrac{2024}{3}\left(\dfrac{3}{2.5}+\dfrac{3}{5.8}+...+\dfrac{3}{62.65}\right)\)
\(=\dfrac{2024}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{62}-\dfrac{1}{65}\right)\)
\(=\dfrac{2024}{3}\left(\dfrac{1}{2}-\dfrac{1}{65}\right)\)
\(=\dfrac{2024}{3}\cdot\dfrac{63}{130}\)
\(=\dfrac{21252}{65}\)
#TiendatzZz
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
giải giúp e gấp đc ko ạ
3(x-12)=0
E cảm ơn mng nhiều ạ !
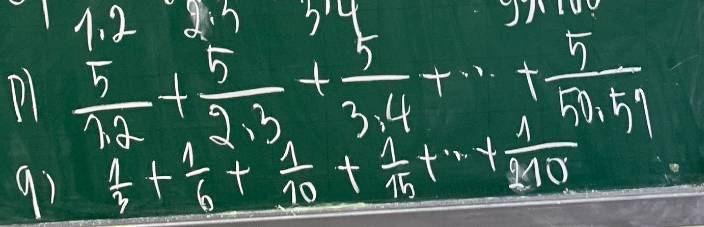
giúp em phần này gấp ạ, xin cảm ơn ạ
 giúp e vs ạ e đang cần gấp cảm ơn m.n nhiều ạ
giúp e vs ạ e đang cần gấp cảm ơn m.n nhiều ạ

Cần giúp mấy phần này gấp ạ. cảm ơn nhiều
mọi người giúp e bài 14;15;16 nhé e đang cần gấp e cảm ơn nhiều ạ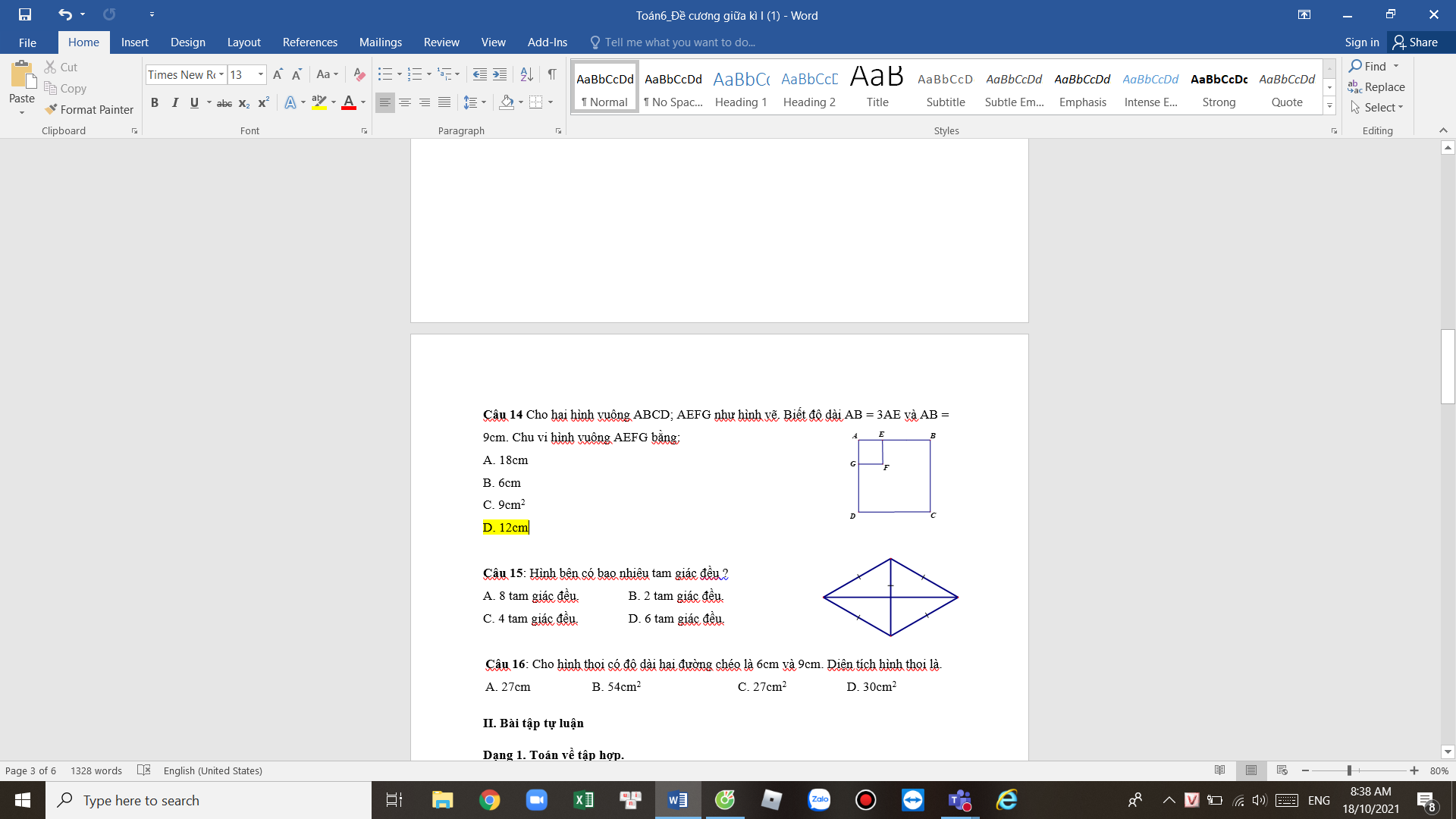
cần giúp nốt phần h trong bài 3 này thui ạ, cảm ơn ạ

Mn giải giúp e bài này vs ạ
Tìm số tự nhiên n biết 3n+4 chia hết cho n-2
E đang cần gấp mong có câu trả lời sớm nhất ạ! E cảm ơn
x^2 - y^2 + 2x - 2y =6 . tìm STN x,y . giúp em với ạ e đang cần gấp ,e xin cảm ơn
Gíup e với ạ , e cần gấp trước tối nay , e cảm ơn nhiều lắm ạ