3.
Cách 1: sử dụng đạo hàm
Xét khai triển:
\(\left(1+x\right)^{2010}=C_{2010}^0+xC_{2010}^1+x^2C_{2010}^2+...+x^nC_{2010}^{2010}\)
Đạo hàm 2 vế:
\(2010.\left(1+x\right)^{2009}=C_{2010}^1+2xC_{2010}^2+3x^2C_{2010}^3+...+2010.x^{2009}C_{2010}^{2010}\)
Cho \(x=1\)
\(\Rightarrow C_{2010}^1+2C_{2010}^2+...+2010.C_{2010}^{2010}=2010.2^{2009}\)
Cách 2:
Ta có: \(k.C_n^k=k.\dfrac{n!}{k!.\left(n-k\right)!}=n.\dfrac{\left(n-1\right)!}{\left(k-1\right)!.\left(n-k\right)!}=n.C_{n-1}^{k-1}\)
Do đó:
\(1.C_n^1=n.C_{n-1}^0\) ; \(2.C_n^2=n.C_{n-1}^1\) ;....; \(n.C_n^n=n.C_{n-1}^{n-1}\)
Cộng vế:
\(1.C_n^1+2.C_n^2+3.C_n^3+...+n.C_n^n=n\left(C_{n-1}^0+C_{n-1}^1+...+C_{n-1}^{n-1}\right)=n.2^{n-1}\)
Thay \(n=2010\)
\(\Rightarrow...\) (đpcm)
5.
Áp dụng công thức: \(C_n^k=C_n^{n-k}\)
\(\Rightarrow C_{2011}^0=C_{2011}^{2011}\)
\(C_{2011}^1=C_{2011}^{2010}\)
...
\(C_{2011}^{1005}=C_{2011}^{1006}\)
Cộng vế:
\(C_{2011}^0+C_{2011}^1+...+C_{2011}^{1005}=C_{2011}^{1006}+...+C_{2011}^{2010}+C_{2011}^{2011}\)
\(\Rightarrow2\left(C_{2011}^0+C_{2011}^1+...+C_{2011}^{1005}\right)=C_{2011}^0+...+C_{2011}^{1005}+C_{2011}^{1006}+...++C_{2011}^{2011}\)
\(\Rightarrow2\left(C_{2011}^0+C_{2011}^1+...+C_{2011}^{1005}\right)=2^{2011}\)
\(\Rightarrow C_{2011}^0+C_{2011}^1+...+C_{2011}^{1005}=\dfrac{2^{2011}}{2}=2^{2010}\)
6.
Áp dụng công thức tương tự bài 5:
\(C_{2n+1}^0=C_{2n+1}^{2n+1}\)
\(C_{2n+1}^2=C_{2n+1}^{2n-1}\)
...
\(C_{2n+1}^{2n}=C_{2n+1}^1\)
Cộng vế:
\(\Rightarrow C_{2n+1}^0+C_{2n+1}^2+...+C_{2n+1}^n=C_{2n+1}^1+C_{2n+1}^3+...+C_{2n+1}^{2n+1}\) (1)
\(\Rightarrow2\left(C_{2n+1}^0+C_{2n+1}^2+...+C_{2n+1}^{2n}\right)=C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^{2n}+C_{2n+1}^{2n+1}=2^{2n+1}\)
\(\Rightarrow C_{2n+1}^0+C_{2n+1}^2+...+C_{2n+1}^{2n}=2^{2n}\) (2)
Lại có:
\(C_{2n+1}^0=C_{2n+1}^{2n+1}\)
\(C_{2n+1}^1=C_{2n+1}^{2n}\)
...
\(C_{2n+1}^n=C_{2n+1}^{n+1}\)
Cộng vế:
\(C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^n=C_{2n+1}^{n+1}+...+C_{2n+1}^{2n+1}\)
\(\Rightarrow2\left(C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^n\right)=C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^{2n}+C_{2n+1}^{2n+1}=2^{2n+1}\)
\(\Rightarrow C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^n=2^{2n}\) (3)
(1);(2);(3) suy ra đpcm
8.
Xét khai triển:
\(\left(1-x\right)^n=C_n^0-xC_n^1+x^2C_n^2-...+\left(-1\right)^n.x^n.C_n^n\)
Thay \(x=\dfrac{1}{3}\)
\(\Rightarrow\left(\dfrac{2}{3}\right)^n=C_n^0-\dfrac{1}{3}C_n^1+\dfrac{1}{3^2}C_n^2-...+\left(-1\right)^n.\dfrac{1}{3^n}C_n^n\)
\(\Rightarrow2^n=3^n\left[C_n^0-\dfrac{1}{3}C_n^1+\dfrac{1}{3^2}C_n^2-...+\left(-1\right)^n.\dfrac{1}{3^n}C_n^n\right]\) (đpcm)
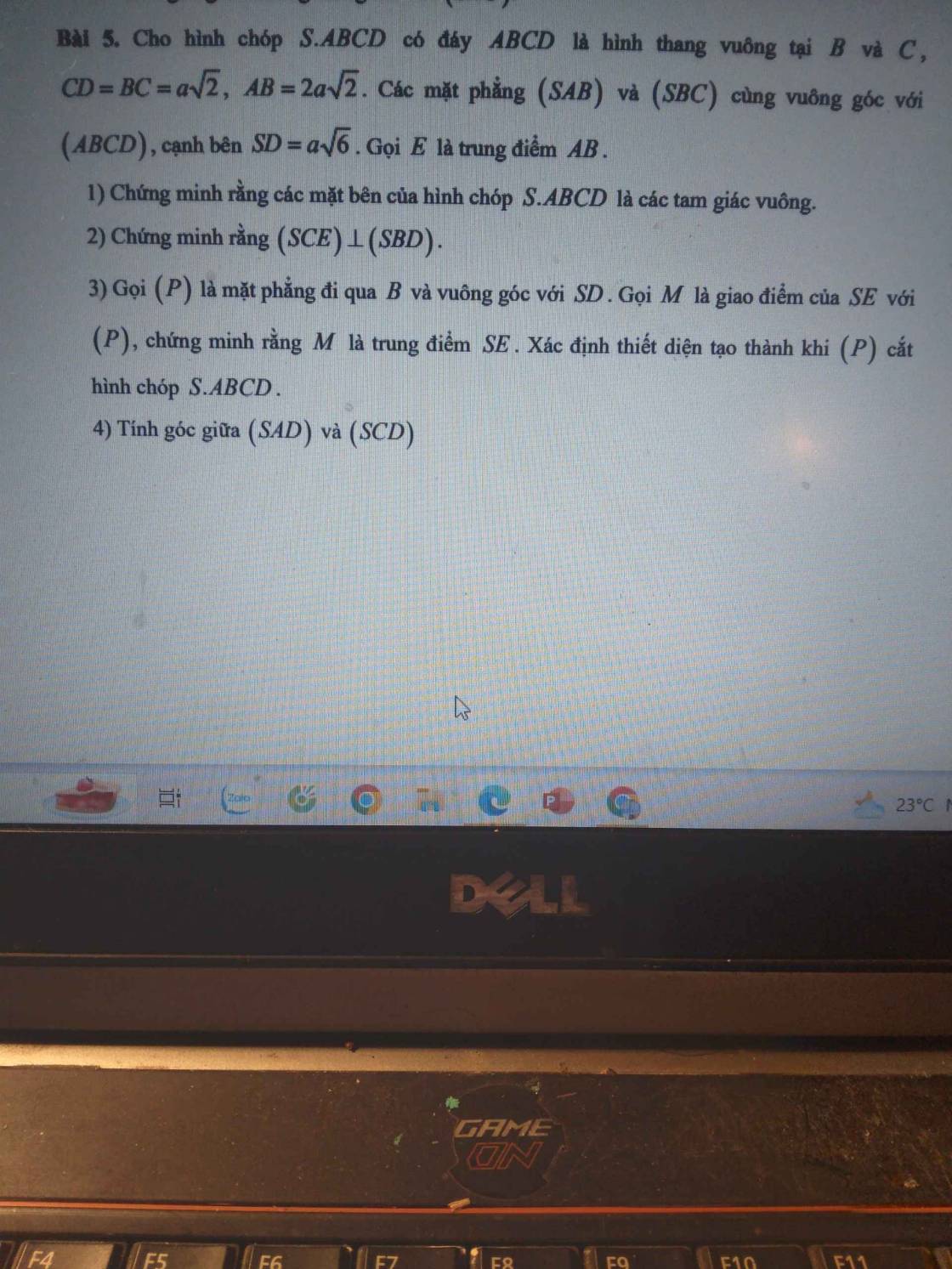giúp em câu 3 4 với ạ. Cần gấp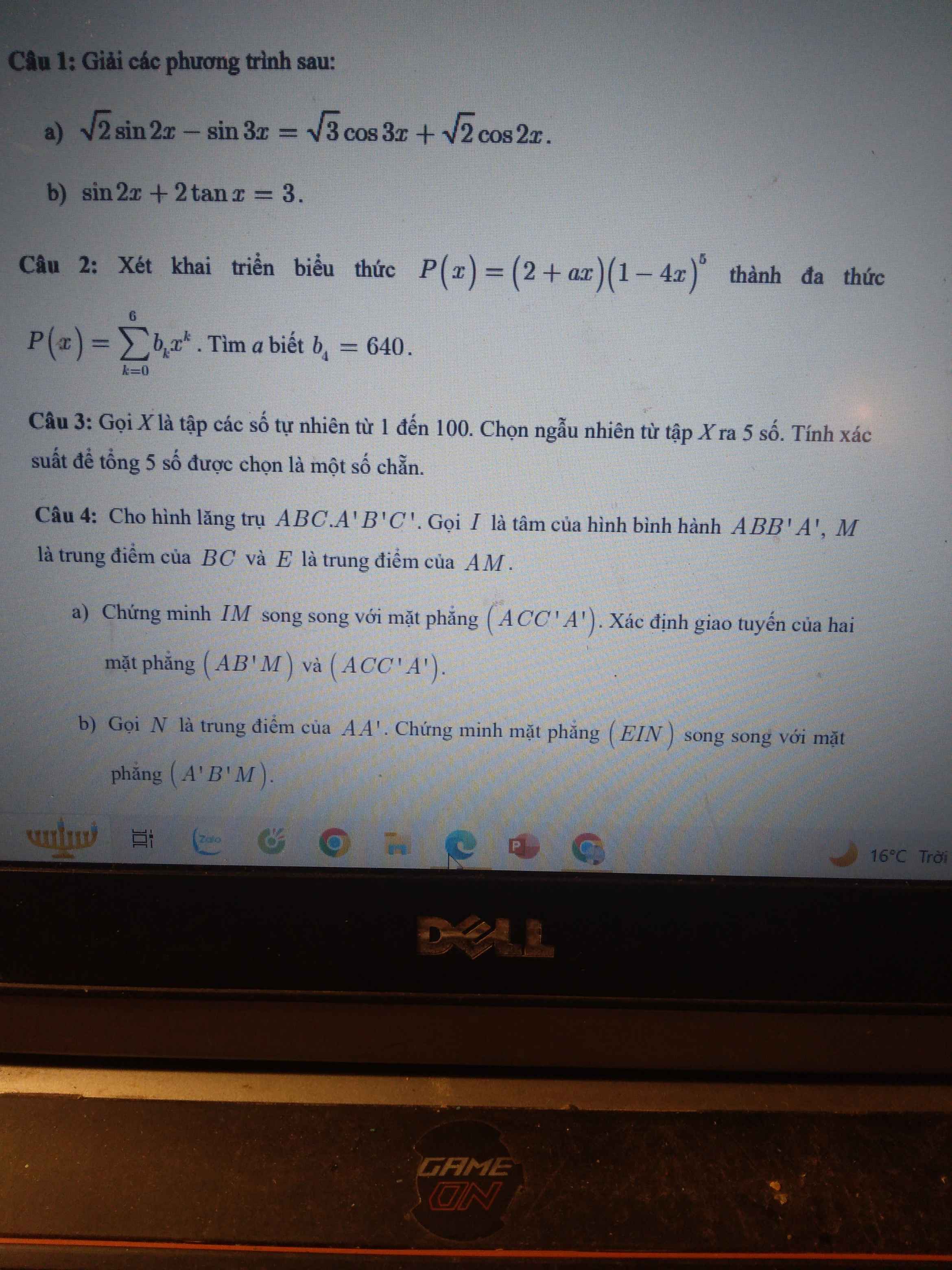
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
