a) \(VT=\left(x+y\right)^2-y^2=x^2+2xy+y^2-y^2\)
\(=x^2+2xy=x\left(x+2y\right)=VP\)
b) \(VT=\left(x^2+y^2\right)^2-\left(2xy\right)^2=x^4+2x^2y^2+y^4-4x^2y^2\)
\(=x^4-2x^2y^2+y^4=\left(x^2-y^2\right)^2=\left[\left(x-y\right)\left(x+y\right)\right]^2\)
\(=\left(x-y\right)^2\left(x+y\right)^2=VP\)
c) \(VT=x^3+3x^2y+3xy^2+y^3-x^3-y^3\)
\(=3x^2y+3xy^2=3xy\left(x+y\right)=VP\)
d) \(VT=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3=2y\left(y^2+3x^2\right)=VP\)


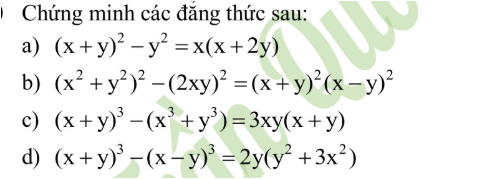 gips minhd vs TT
gips minhd vs TT










