- Chia cả tử và mẫu cho n 2 ( n 2 là lũy thừa bậc cao nhất của n trong mẫu thức), ta được:
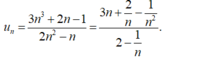
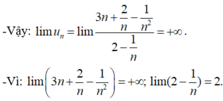
Chọn C
- Chia cả tử và mẫu cho n 2 ( n 2 là lũy thừa bậc cao nhất của n trong mẫu thức), ta được:
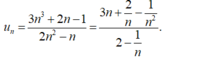
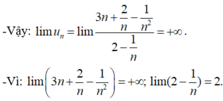
Chọn C
Cho dãy số ( u n ) xác định bởi u 1 = 1 u n + 1 = 2 u n + 3 u n + 2 v ớ i n ≥ 1
a) Chứng minh rằng u n > 0 với mọi n.
b) Biết ( u n ) có giới hạn hữu hạn. Tìm giới hạn đó.
Tính giới hạn của dãy số B = l i m n 6 + n + 1 3 - 4 n 4 + 2 n - 1 ( 2 n + 3 ) 2
A. +∞
B. -∞
C. 3
D. -3/4
Câu 1: Tính giới hạn
a, lim\(\dfrac{2-5^{n-2}}{3^n=2.5^n}\) b,lim\(\dfrac{2-5^{n+2}}{3^n-2.5^n}\)
Câu 2 :CMR :\(x^4+x^3-3x^2+x+1=0\) có ít nhất một nghiệm âm lớn hơn -1
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4^{n+1}}{3^{n+2}+4^n}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4.2^{n+1}-3}{3.2^n+4^n}\right)\)
3) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{2-5^{n-2}}{3^n+2.5^n}\right)\)
1) Tính giới hạn \(K=\lim\limits_{n\rightarrow\infty}\left(\dfrac{3.2^n-3^n}{2^{n+1}+3^{n+1}}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4^{n+1}}{3^{n+2}+4^n}\right)\)
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4^{n+1}}{3^{n+2}+4^n}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n+1}{2^n-1}\right)\)
Cho hàm số f(n)= 1 1 . 2 . 3 + 1 2 . 3 . 4 + . . . + 1 n . ( n + 1 ) . ( n + 2 ) = n ( n + 3 ) 4 ( n + 1 ) ( n + 2 ) , n ∈ N * . Kết quả giới hạn lim ( 2 n 2 + 1 - 1 ) f ( n ) 5 n + 1 = a b ( b ∈ Z ) . Giá trị của a 2 + b 2 là
A.101
B.443
C.363
D.402
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\sqrt[3]{n^3+3n^2+1}-n\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{4n^2+1}-\sqrt[3]{8n^3+n}\right)\)