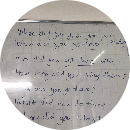Giari gấp giúp mình vs ạ
Bài 1:
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
b: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
Ta có: AH\(\perp\)BC
mà H là trung điểm của BC
nên AH là đường trung trực của BC
Câu 2:
a: Xét ΔNMD và ΔNED có
NM=NE
\(\widehat{MND}=\widehat{END}\)
ND chung
Do đó: ΔNMD=ΔNED
Xét ΔNME có NM=NE
nên ΔNME cân tại N
b: Ta có: ΔNMD=ΔNED
=>DM=DE
=>D nằm trên đường trung trực của ME(1)
Ta có: NM=NE
=>N nằm trên đường trung trực của ME(2)
Từ (1),(2) suy ra DN là đường trung trực của EM
Đúng 2
Bình luận (0)
