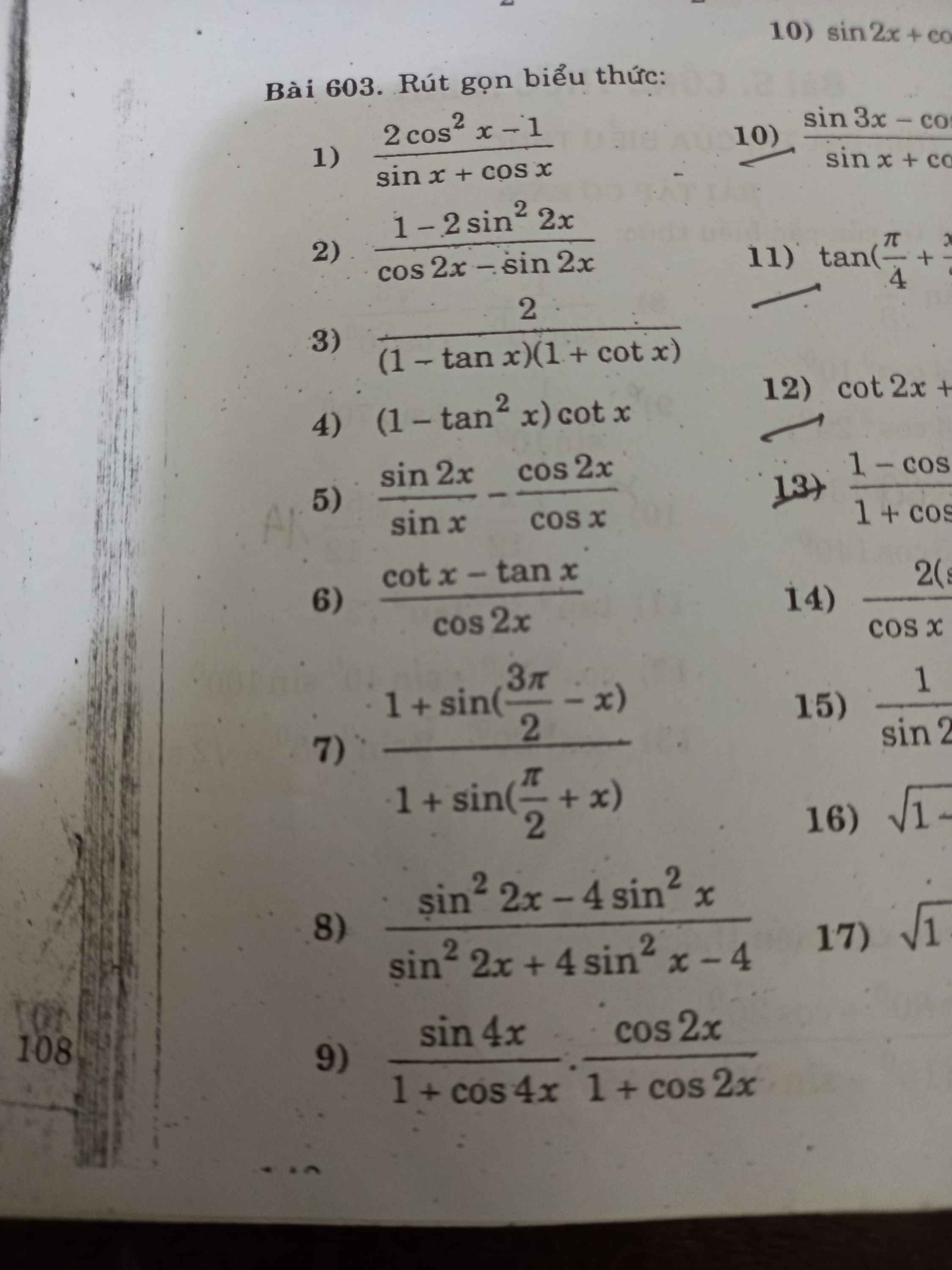Câu 1: Xét ΔABC có \(cosA=\dfrac{b^2+c^2-a^2}{2\cdot b\cdot c}\)
=>\(b^2+c^2-a^2=2\cdot b\cdot c\cdot cosA\)
=>\(a^2=b^2+c^2-2bc\cdot cosA\)
=>Chọn B
Câu 2: Xét ΔABC có
\(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
=>\(\dfrac{8^2+10^2-AB^2}{2\cdot8\cdot10}=cos60=\dfrac{1}{2}\)
=>\(164-AB^2=80\)
=>\(AB^2=164-80=84\)
=>\(AB=\sqrt{84}=2\sqrt{21}\)
=>Chọn D
Câu 3:
Xét ΔABC có \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(\dfrac{6^2+8^2-BC^2}{2\cdot6\cdot8}=cos60=\dfrac{1}{2}\)
=>\(100-BC^2=48\)
=>\(BC^2=100-48=52\)
=>\(BC=\sqrt{52}=2\sqrt{13}\)
=>Chọn A
Câu 4: Xét ΔABC có \(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
=>\(\dfrac{8^2+5^2-AC^2}{2\cdot8\cdot5}=cos60=\dfrac{1}{2}\)
=>\(64+25-AC^2=40\)
=>\(AC^2=49=7^2\)
=>AC=7
=>Chọn A
Câu 5: Xét ΔABC có \(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
=>\(\dfrac{9^2+8^2-AC^2}{2\cdot9\cdot8}=cos60=\dfrac{1}{2}\)
=>\(81+64-AC^2=72\)
=>\(AC^2=81+64-72=64+9=73\)
=>\(AC=\sqrt{73}\)
=>Chọn A
Câu 6: Xét ΔABC có \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(\dfrac{2^2+1^2-BC^2}{2\cdot2\cdot1}=cos60=\dfrac{1}{2}\)
=>\(5-BC^2=\dfrac{4}{2}=2\)
=>\(BC^2=3\)
=>\(BC=\sqrt{3}\)
=>Chọn C
Câu 7; Xét ΔABC có \(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
=>\(\dfrac{8^2+3^2-AC^2}{2\cdot8\cdot3}=cos60=\dfrac{1}{2}\)
=>\(64+9-AC^2=8\cdot3=24\)
=>\(AC^2=73-24=49\)
=>AC=7
=>Chọn C
Câu 8: Xét ΔABC có \(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
=>\(\dfrac{\left(\sqrt{3}\right)^2+2^2-AB^2}{2\cdot\sqrt{3}\cdot2}=cos150=\dfrac{-\sqrt{3}}{2}\)
=>\(7-AB^2=4\sqrt{3}\cdot\dfrac{-\sqrt{3}}{2}=2\cdot\left(-3\right)=-6\)
=>\(AB^2=13\)
=>\(AB=\sqrt{13}\)
=>Chọn A
Câu 9: Xét ΔABC có \(cosA=\dfrac{BA^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(\dfrac{7^2+5^2-BC^2}{2\cdot7\cdot5}=\dfrac{4}{5}\)
=>\(49+25-BC^2=2\cdot7\cdot5\cdot\dfrac{4}{5}=2\cdot7\cdot4=56\)
=>\(BC^2=49+25-56=18\)
=>\(BC=3\sqrt{2}\)
=>Chọn A


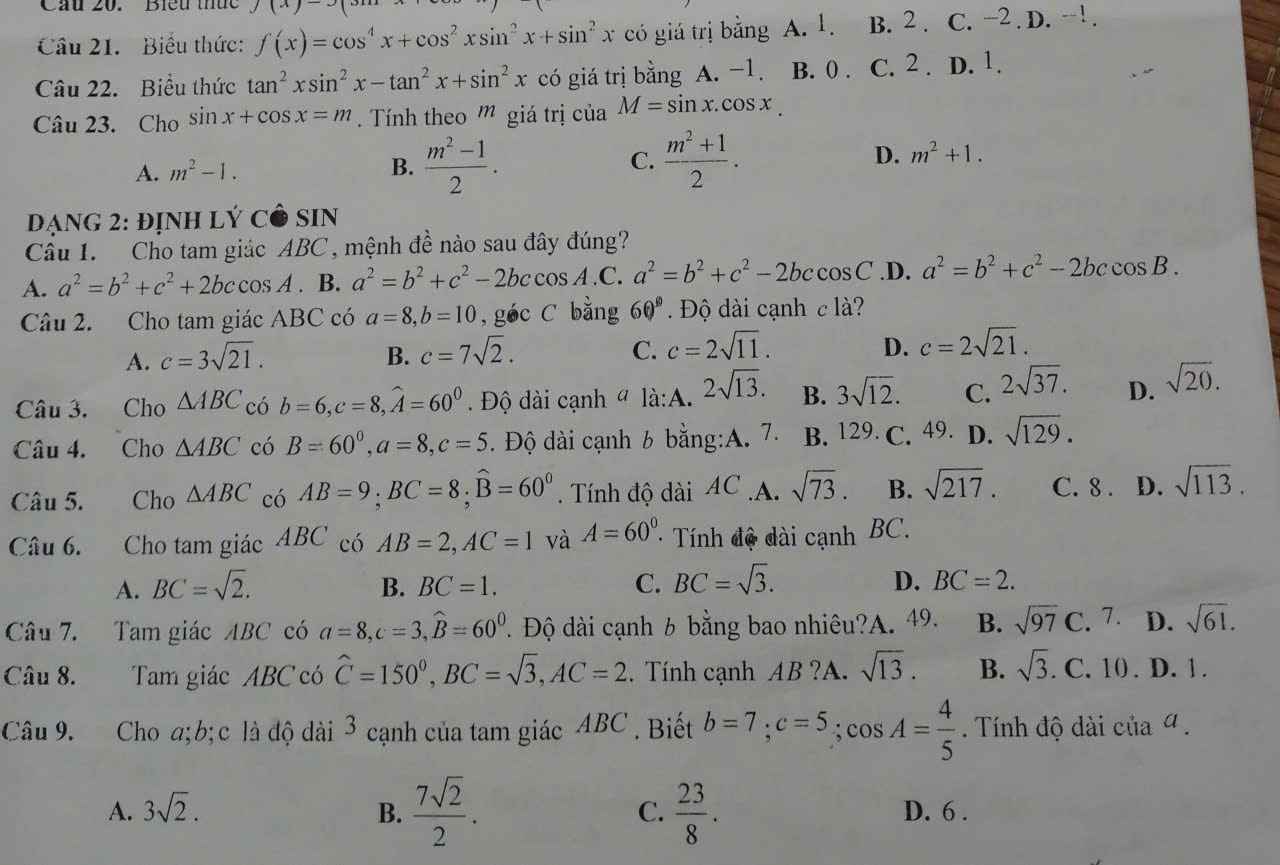







 Giải giúp mình phần trắc nghiệm với ạ
Giải giúp mình phần trắc nghiệm với ạ
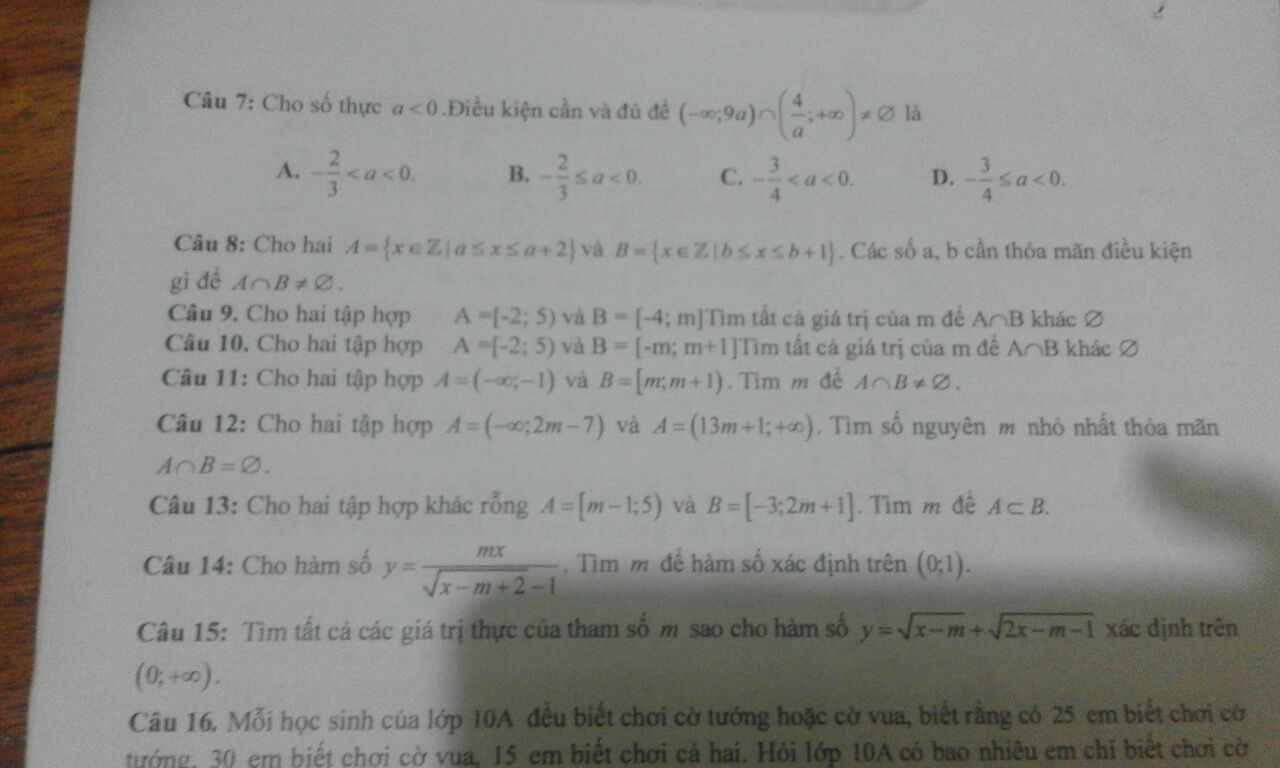 GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!