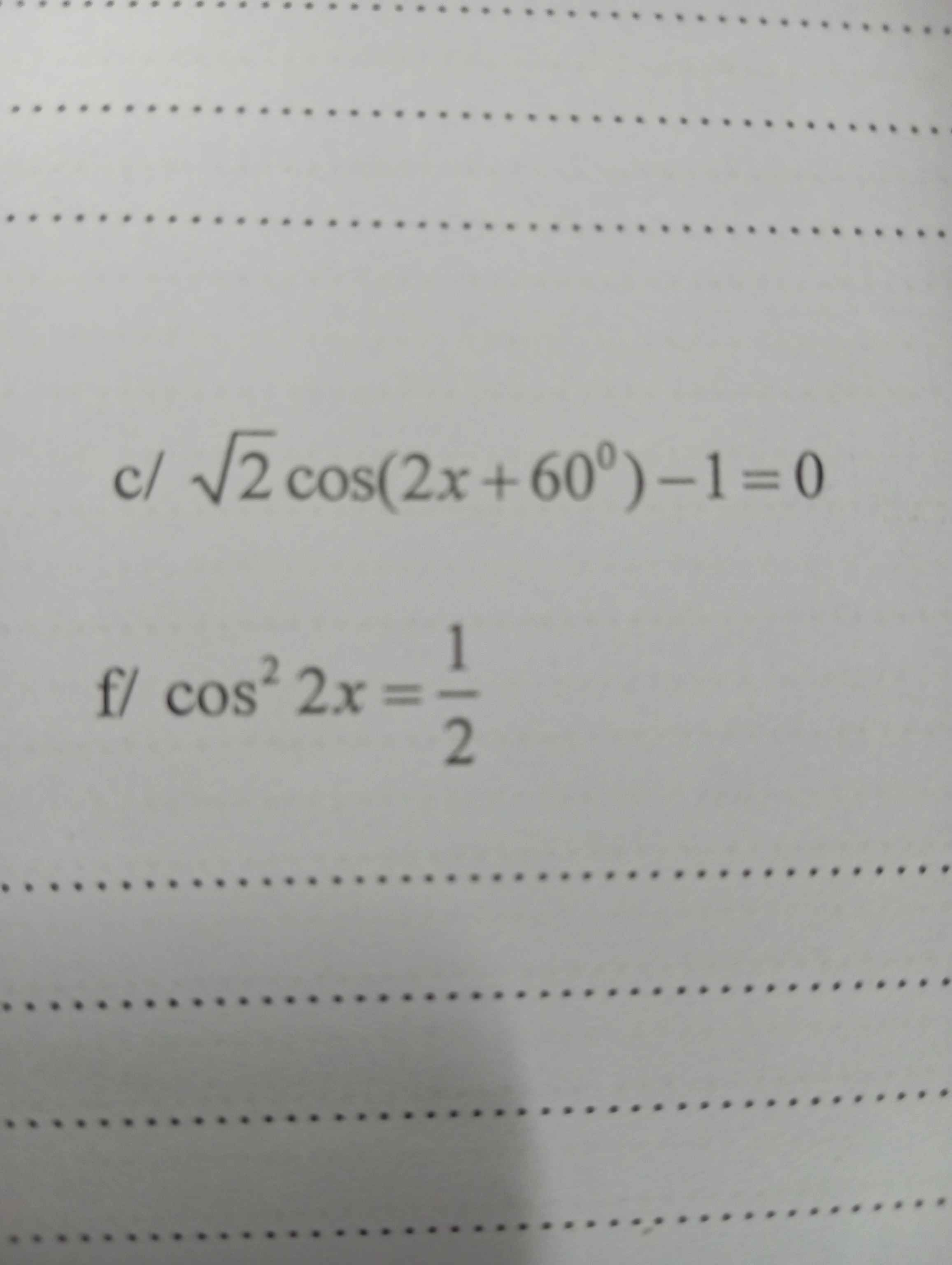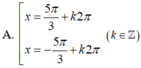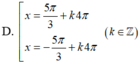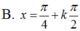c: \(\sqrt{2}\cdot cos\left(2x+60^0\right)-1=0\)
=>\(cos\left(2x+60^0\right)=\dfrac{1}{\sqrt{2}}\)
=>\(\left[{}\begin{matrix}2x+60^0=45^0+k\cdot360^0\\2x+60^0=-45^0+k\cdot360^0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2x=-15^0+k\cdot360^0\\2x=-105^0+k\cdot360^0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-7,5^0+k\cdot180^0\\x=-52,5^0+k\cdot180^0\end{matrix}\right.\)
f: \(cos^22x=\dfrac{1}{2}\)
=>\(\dfrac{1+cos4x}{2}=\dfrac{1}{2}\)
=>1+cos4x=1
=>cos4x=0
=>\(4x=\dfrac{\Omega}{2}+k\Omega\)
=>\(x=\dfrac{\Omega}{8}+\dfrac{k\Omega}{4}\)