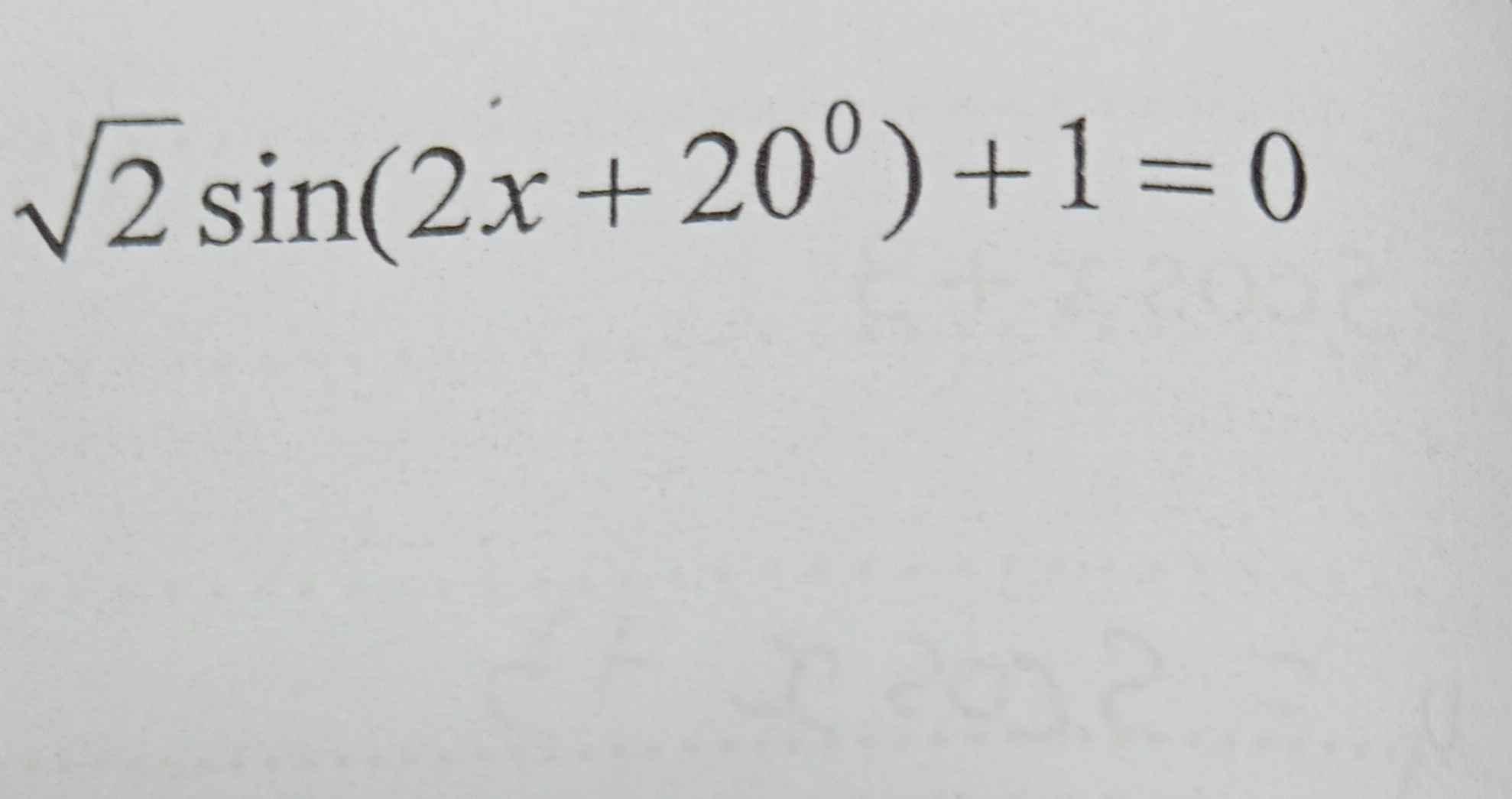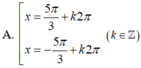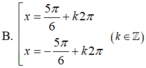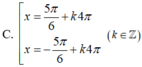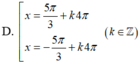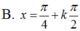Question

  Giải phương trình lượng giác

Answer 1

\(\sqrt{2}\cdot sin\left(2x+20^0\right)+1=0\)

=>\(\sqrt{2}\cdot sin\left(2x+20^0\right)=-1\)

=>\(sin\left(2x+20^0\right)=-\dfrac{1}{\sqrt{2}}\)

=>\(\left[{}\begin{matrix}2x+20^0=-45^0+k\cdot360^0\\2x+20^0=180^0+45^0+k\cdot360^0=225^0+k\cdot360^0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}2x=-65^0+k\cdot360^0\\2x=205^0+k\cdot360^0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-32,5^0+k\cdot180^0\\x=102,5^0+k\cdot180^0\end{matrix}\right.\)