Điều kiện xác định:
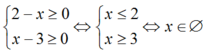
Vậy phương trình vô nghiệm.
Điều kiện xác định:
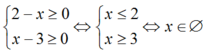
Vậy phương trình vô nghiệm.
a, giải phương trình : 4x²+√2x+3=8x+1
B, giải hệ phương trình :
{√x+y+1+(x+2y)=4(x+y) ²+√3*√x+y
X-4y-3=(2y)²-√2-x²
\(\left(x-2\right)\sqrt{x^2-2x-3}\le x^2-4\)
Giải bất phương trình
Giải phương trình (x-3)căn(1+x)-x căn(4-x)=2x^2-6x-3
Giải bất phương trình: \(\sqrt[3]{x+1}+\sqrt{2x+4}< 3-x\sqrt{2}\)
Giải phương trình: \(\sqrt{x+5-2\sqrt{x+4}}=3\sqrt{x+4}-2\)
giải phương trình :
\(9\left(\sqrt{x+1}+\sqrt{x-2}\right)+1=4\left(\sqrt{\left(x+1\right)^3}-\sqrt{\left(x-2\right)^3}\right)\)
- giải các bất phương trình sau:
a) (\(3x^2-7x+4\))(\(x^2+x+4\))\(>0\)
b) \(x^3-13x^2+42x-36>0\)
c) \(x\left(x+5\right)\le2\left(x^2+2\right)\)
Giải các bất phương trình sau:
a)\(\left(x^2+3x-4\right)\left(3-2x\right)\)<0
b) \(\dfrac{x^2+3x+4}{x^2-2}\ge0\)
c) \(\dfrac{x\left(x^2+4x+4\right)}{x^2-1}\ge0\)
Giải hệ phương trình :
\(\left\{{}\begin{matrix}\sqrt{3+2x^2y-x^4y^2}+x^4\left(1-2x^2\right)=y^2\\1+\sqrt{1+\left(x-y\right)^2}=x^3\left(x^3-x+2y^2\right)\end{matrix}\right.\)
Giải các phương trình, bất phương trình sau:
1) \(\sqrt{3x+7}-5< 0\)
2) \(\sqrt{-2x-1}-3>0\)
3) \(\dfrac{\sqrt{3x-2}}{6}-3=0\)
4) \(-5\sqrt{-x-2}-1< 0\)
5) \(-\dfrac{2}{3}\sqrt{-3-x}-3>0\)