Điều kiện xác định:
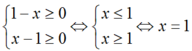
Xét x = 1: VT (2) = 1; VP (2) = 2.
Vậy x = 1 không phải nghiệm của (2) nên phương trình (2) vô nghiệm.
Vậy phương trình đã cho vô nghiệm.
Điều kiện xác định:
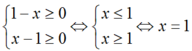
Xét x = 1: VT (2) = 1; VP (2) = 2.
Vậy x = 1 không phải nghiệm của (2) nên phương trình (2) vô nghiệm.
Vậy phương trình đã cho vô nghiệm.
a, giải phương trình : 4x²+√2x+3=8x+1
B, giải hệ phương trình :
{√x+y+1+(x+2y)=4(x+y) ²+√3*√x+y
X-4y-3=(2y)²-√2-x²
giải phương trình: (x + 1)( |x| - 1)= 1/2
giải phương trình |x^2 - 2x -1|== x-1
giải phương trình √x^2 -x +1 = 1 -2x
giải bất phương trình sau :
a) (1-2x)(x^2-x-20)>0
b)\(\sqrt{x^2-x-2}\) \(< x-1\)
Giải phương trình x + 5 - 4 x + 1 + x + 1 = 2
![]()
![]()
![]()
![]()
Giải bất phương trình sau: |x + 2| + |-2x + 1| ≤ x + 1
Giải phương trình:
x+1+√(x^2-4x+1)=3√x
Giải phương trình sau :
\(x^2+x+3=\left(x+1\right)\sqrt{x-1}\)
Thanks nhìu ạ!!!!!!!!!!