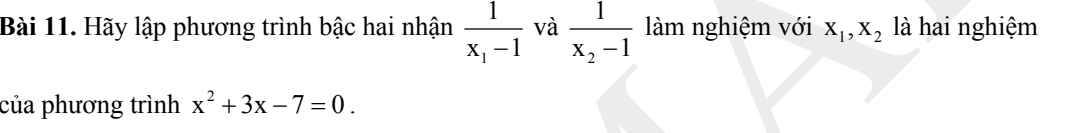bài IV:
1: Xét tứ giác OBAC có \(\widehat{OBA}+\widehat{OCA}+\widehat{BOC}+\widehat{BAC}=360^0\)
=>\(\widehat{BAC}+120^0+90^0+90^0=360^0\)
=>\(\widehat{BAC}=60^0\)
Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC và AO là phân giác của góc BAC
Xét ΔABC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔABC đều
2: Xét (O) có
EB,EM là các tiếp tuyến
DO đó: EB=EM
Xét (O) có
FM,FC là các tiếp tuyến
Do đó: FM=FC
Ta có: AO là phân giác của góc BAC
=>\(\widehat{BAO}=\widehat{CAO}=\dfrac{60^0}{2}=30^0\)
Xét ΔOBA vuông tại B có \(tanBAO=\dfrac{OB}{BA}\)
=>\(\dfrac{R}{BA}=tan30=\dfrac{1}{\sqrt{3}}\)
=>\(BA=R\sqrt{3}\)
Chu vi tam giác AEF là:
AE+EF+AF
=AE+EM+FM+AF
=AE+EB+AF+FC
=AB+AC
=2AB
\(=2R\sqrt{3}\)