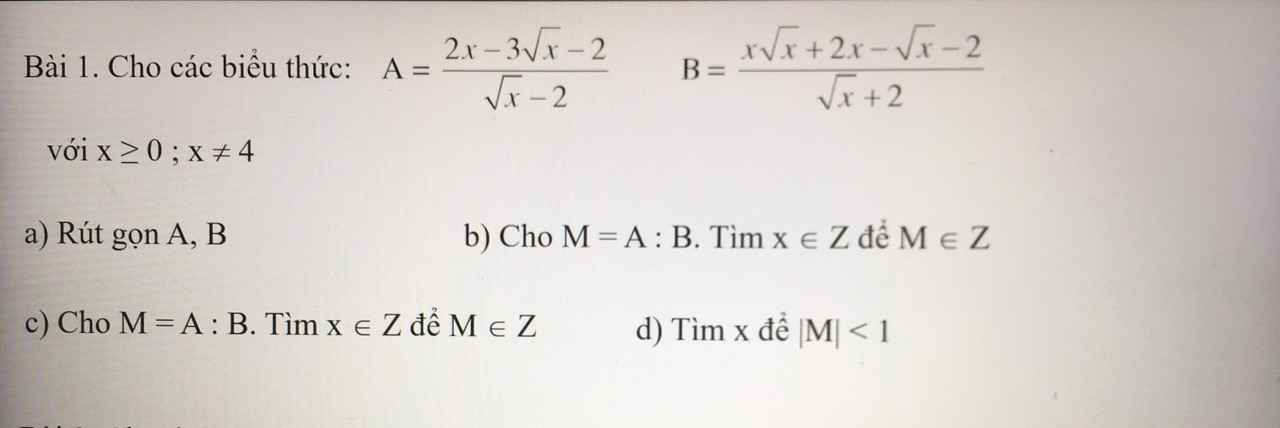\(a,ĐK:x\ge0;x\ne4\\ A=\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\sqrt{x}-2}=2\sqrt{x}+1\\ B=\dfrac{\left(x-1\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+2}=x-1\\ b,M=A:B=\dfrac{2\sqrt{x}+1}{x-1}=\dfrac{2\left(\sqrt{x}+1\right)-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ M=\dfrac{2}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\in Z\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}-1\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\\sqrt{x}+1\inƯ\left(1\right)=\left\{-1;1\right\}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}\in\left\{0;2;3\right\}\left(\sqrt{x}\ge0\right)\\\sqrt{x}=0\left(\sqrt{x}\ge0\right)\end{matrix}\right.\Leftrightarrow x=0\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Giải hộ mình con này với,mình đang cần gấp.

giải hộ mình với không cần làm bài 4 đâu ạ
mình đang cần gấp
mọi người ai giải hộ em câu này với em đang cần gấp câu này em cảm ơn ạ!

MN giải hộ em bài này,đang cần gấp.
giúp mình giải bài này với ạ, mình đang cần gấp, mình 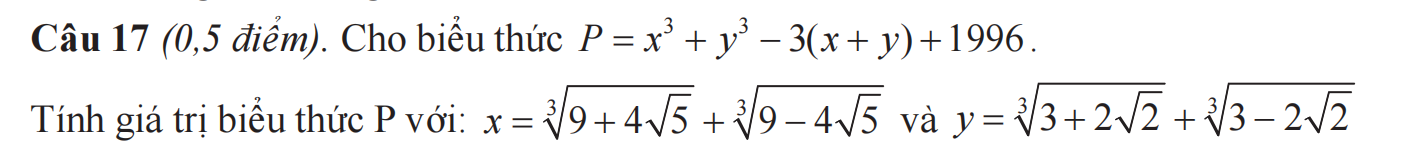 cảm ơn
cảm ơn
Đang cần bài này gấp mong MN giải hộ em.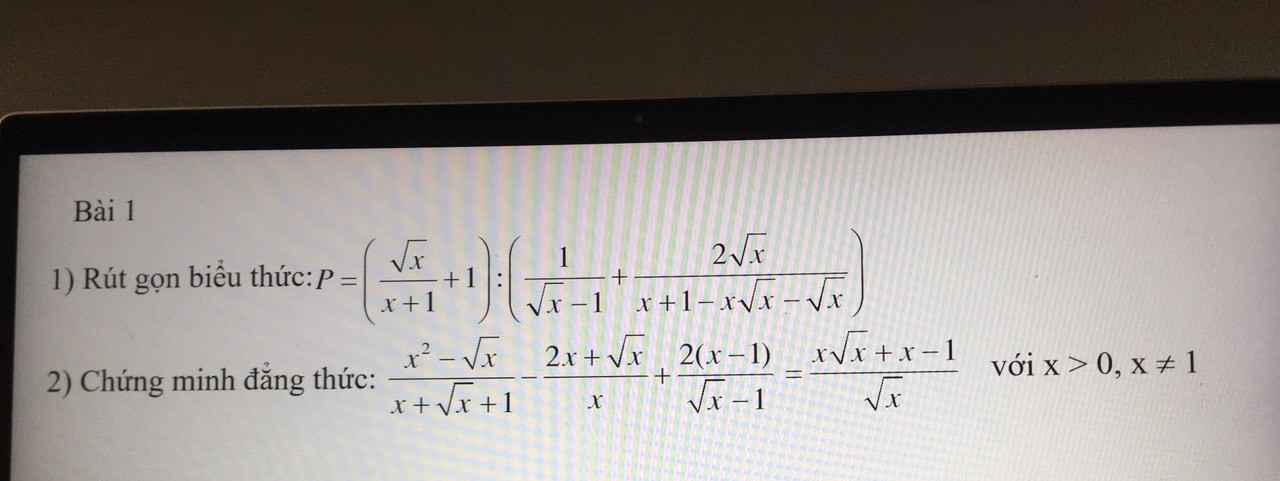
AI giúp mình giải chi tiết câu này với mình đang cần gấp
Đọc tiếp
AI giúp mình giải chi tiết câu này với mình đang cần gấp
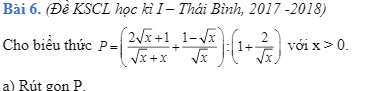
giải giúp mình câu này với mình đang cần gấp, mình cảm ơn rất nhiều