Lời giải:
\(B=\left[\frac{6\sqrt{x}+6}{(\sqrt{x}-1)(\sqrt{x}+3)}-\frac{(\sqrt{x}+2)(\sqrt{x}+3)}{(\sqrt{x}-1)(\sqrt{x}+3)}\right].(\sqrt{x}+3)\)
\(=\frac{6\sqrt{x}+6-(x+5\sqrt{x}+6)}{(\sqrt{x}-1)(\sqrt{x}+3)}.(\sqrt{x}+3)=\frac{-\sqrt{x}(\sqrt{x}-1)}{(\sqrt{x}-1)(\sqrt{x}+3)}.(\sqrt{x}+3)=-\sqrt{x}\)
Do đó:
\(P=AB=\frac{\sqrt{x}}{\sqrt{x}-3}\)
\(P=1+\frac{3}{\sqrt{x}-3}\)
Để $P$ max thì $\sqrt{x}-3>0$ và nhỏ nhất.
$\sqrt{x}-3>0\Leftrightarrow x>9$. $x$ nguyên nhỏ nhất khi $x=10$
Vậy $P_{\max}=1+\frac{3}{\sqrt{10}-3}$













 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
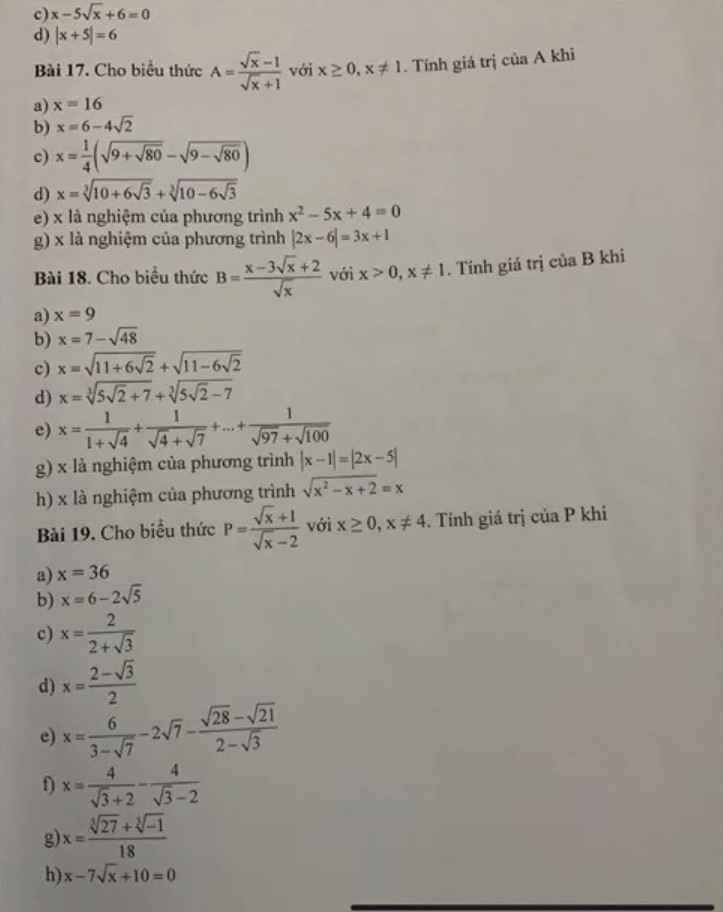 giải hộ mình bài 19 ạ
giải hộ mình bài 19 ạ





