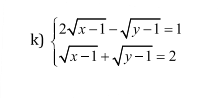+)ĐK xác định của hệ phương trình trên là: \(\left[{}\begin{matrix}x\ge0\\y\ge0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\sqrt{x}+\sqrt{y}=3\\\sqrt{xy}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{xy}+\sqrt{y}^2=3\sqrt{y}\\\sqrt{xy}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{xy}=3\sqrt{y}-\sqrt{y}^2=3\sqrt{y}-\left|y\right|\\\sqrt{xy}=2\end{matrix}\right.\)
➢Do hệ phương trình trên, ta có: \(3\sqrt{y}-\left|y\right|=2\\ \Leftrightarrow\left|y\right|=3\sqrt{y}-2\\ \Leftrightarrow\left[{}\begin{matrix}y=3\sqrt{y}-2\\y=-\left(3\sqrt{y}-2\right)=2-3\sqrt{y}\end{matrix}\right.\\\Leftrightarrow\left[{}\begin{matrix}y-3\sqrt{y}+2=0\\y+3\sqrt{y}-2=0\end{matrix}\right. \)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{y}^2-2\sqrt{y}-\sqrt{y}+2=0\\\sqrt{y}^2+2\sqrt{y}+\sqrt{y}+2=0\end{matrix}\right.\\\Leftrightarrow\left[{}\begin{matrix}\left(\sqrt{y}-2\right)\left(\sqrt{y}-1\right)=0\\\left(\sqrt{y}+2\right)\left(\sqrt{y}+1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{y}-2=0\\\sqrt{y}-1=0\end{matrix}\right.\) vì với mọi x thì \(\sqrt{y}\ge0\Leftrightarrow\left[{}\begin{matrix}\sqrt{y}+2\ge2>0\\\sqrt{y}+1\ge1>0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{y}=2\\\sqrt{y}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=2^2=4\\y=1^2=1\end{matrix}\right.\)
Với \(y=4\) thì \(\sqrt{xy}=2\Leftrightarrow xy=2^2=4\Leftrightarrow4x=4\Leftrightarrow x=1\)
\(y=1\) thì \(\sqrt{xy}=2\Leftrightarrow xy=2^2=4\Leftrightarrow1x=4\Leftrightarrow x=4\)
➤ \(\left\{{}\begin{matrix}y=1\\x=4\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}y=4\\x=1\end{matrix}\right.\)
\(\sqrt{xy}=2\Leftrightarrow xy=2^2=4\Leftrightarrow4x=4\Leftrightarrow x=1\)