<=>\(x^4-8x^2-9=0\)
đặt \(t=x^2\left(t\ge0\right)\)
pt thành \(t^2-8t-9=0\)
<=>\(\left(t+1\right)\left(t-9\right)\)
<=>\(\left[{}\begin{matrix}t=-1\\t=9\end{matrix}\right.\)
so với đk của t=>t=9
vậy \(x^2=9\)
<=>x=\(\pm9\)
<=>\(x^4-8x^2-9=0\)
đặt \(t=x^2\left(t\ge0\right)\)
pt thành \(t^2-8t-9=0\)
<=>\(\left(t+1\right)\left(t-9\right)\)
<=>\(\left[{}\begin{matrix}t=-1\\t=9\end{matrix}\right.\)
so với đk của t=>t=9
vậy \(x^2=9\)
<=>x=\(\pm9\)
Giải hệ phương trình: 2 x − y = 3 x 2 + y = 5
: Giải phương trình rồi kiểm nghiệm hệ vi-ét:
a. 5x2 + 2x -16 =0 b.3x2 -2x -5 =0
Giải pt: \(\sqrt{x-7}\) + \(\sqrt{9-x}\) = 3x2- 48x +194
Giải các phương trình:
a ) 3 x 4 – 12 x 2 + 9 = 0 ; b ) 2 x 4 + 3 x 2 – 2 = 0 ; c ) x 4 + 5 x 2 + 1 = 0.
Bài 1 (2đ): Giải phương trình và hệ phương trình sau:
a)3x2 – 26x + 49 = 0
b) 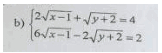
giả phương trình sau: 3x4-11x2+10=0
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
a ) 2 x 2 − 7 x + 3 = 0 b ) 6 x 2 + x + 5 = 0 c ) 6 x 2 + x − 5 = 0 d ) 3 x 2 + 5 x + 2 = 0 e ) y 2 − 8 y + 16 = 0 f ) 16 z 2 + 24 z + 9 = 0
giải hệ phương trình:
(1) x^2+y^2=1
(2) x^2-x=y^2-y
a) giải hpt
b) cho pt bâc hai ax^2+bx+c=0. gọi hai nghiệm là x1 x2. lập pt bậc hai có hai nghiệm là 2x1+3x2 & 3x1+2x2.
giúp mình câu b? tksss
a ) Giải hệ pt:
\(2x^4+3x^2-2=0\)
b ) Cho phương trình x2 - (m+1)x +m =0 . tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm phân biệt x1, x2 thoă mãn x1 = 3x2