e.
$x^4-4x^3-8x^2+8x=0$
$\Leftrightarrow x(x^3-4x^2-8x+8)=0$
$\Leftrightarrow x[x^2(x+2)-6x(x+2)+4(x+2)]=0$
$\Leftrightarrow x(x+2)(x^2-6x+4)=0$
$\Leftrightarrow x=0$ hoặc $x+2=0$ hoặc $x^2-6x+4=0$
$\Leftrightarrow x=0$ hoặc $x=-2$ hoặc $x^2-6x+4=0$
Xét riêng pt $x^2-6x+4=0$
$\Leftrightarrow (x-3)^2=5$
$\Leftrightarrow x-3=\pm \sqrt{5}$
$\Leftrightarrow x=3\pm \sqrt{5}$
Vậy.........
f.
$2x^2+3xy+y^2=0$
$\Leftrightarrow (2x^2+2xy)+(xy+y^2)=0$
$\Leftrightarrow 2x(x+y)+y(x+y)=)$
$\Leftrightarrow (x+y)(2x+y)=0$
$\Leftrightarrow x+y=0$ hoặc $2x+y=0$
$\Leftrightarrow x=-y$ hoặc $x=\frac{-y}{2}$
g.
$2x^4-x^3-9x^2+13x-5=0$
$\Leftrightarrow (2x^4-2x^3)+(x^3-x^2)-(8x^2-8x)+(5x-5)=0$
$\Leftrightarrow 2x^3(x-1)+x^2(x-1)-8x(x-1)+5(x-1)=0$
$\Leftrightarrow (x-1)(2x^3+x^2-8x+5)=0$
$\Leftrightarrow (x-1)[2x^2(x-1)+3x(x-1)-5(x-1)]=0$
$\Leftrightarrow (x-1)^2(2x^2+3x-5)=0$
$\Leftrightarrow (x-1)^2[2x(x-1)+5(x-1)]=0$
$\Leftrightarrow (x-1)^3(2x+5)=0$
$\Leftrightarrow x-1=0$ hoặc $2x+5=0$
$\Leftrightarrow x=1$ hoặc $x=\frac{-5}{2}$
h.
$(x+1)(x+3)(x+5)(x+7)+15=0$
$\Leftrightarrow [(x+1)(x+7)][(x+3)(x+5)]+15=0$
$\Leftrightarrow (x^2+8x+7)(x^2+8x+15)+15=0$
Đặt $x^2+8x+7=a$ thì pt trở thành:
$a(a+8)+15=0$
$\Leftrightarrow a^2+8a+15=0$
$\Leftrightarrow (a+3)(a+5)=0$
$\Leftrightarrow a+3=0$ hoặc $a+5=0$
$\Leftrightarrow x^2+8x+10=0$ hoặc $x^2+8x+12=0$
$\Leftrightarrow (x+4)^2=6$ hoặc $(x+4)^2=4$
$\Leftrightarrow x+4=\pm \sqrt{6}$ hoặc $x+4=\pm 2$
$\Leftrightarrow x\in\left\{\pm \sqrt{6}-4; -6; -2\right\}$

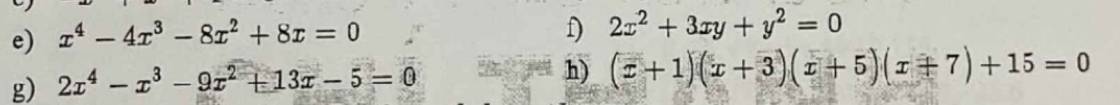 giải hệ phương trình:(
giải hệ phương trình:(








