a) Xét ΔBDC: M là trung điểm của BC, HC=HD
=> H là trung điểm của CD.
=> HM là đường trung bình của ΔBDC
=> HM//BD.
Mà HM \(\perp\) EF => BD \(\perp\) EF (Quan hệ song song vuông góc)
Xét ΔBHD: BE \(\perp\) DH; HE \(\perp\) BD ( EF \(\perp\) BD (cmt) )
=> E là trực tâm của ΔBHD (đpcm)
b) Nối D với E.
Ta có E là trực tâm ΔBHD (cmt)
=> DE \(\perp\) BH
Mà AC vuông góc BH => DE//AC (Quan hệ song song vuông góc) hay DE//CF
=> \(\widehat{EDH}=\widehat{FCH}\) (Cặp góc So le trong)
Xét ΔDEH và ΔCFH:
\(\widehat{DHE}=\widehat{CHF}\) (Đối đỉnh)
HD=HC
\(\widehat{EDH}=\widehat{FCH}\) (cmt)
⇒ΔDEH=ΔCFH (g.c.g)
⇒HE=HF (2 cạnh tương ứng)( Đpcm.)
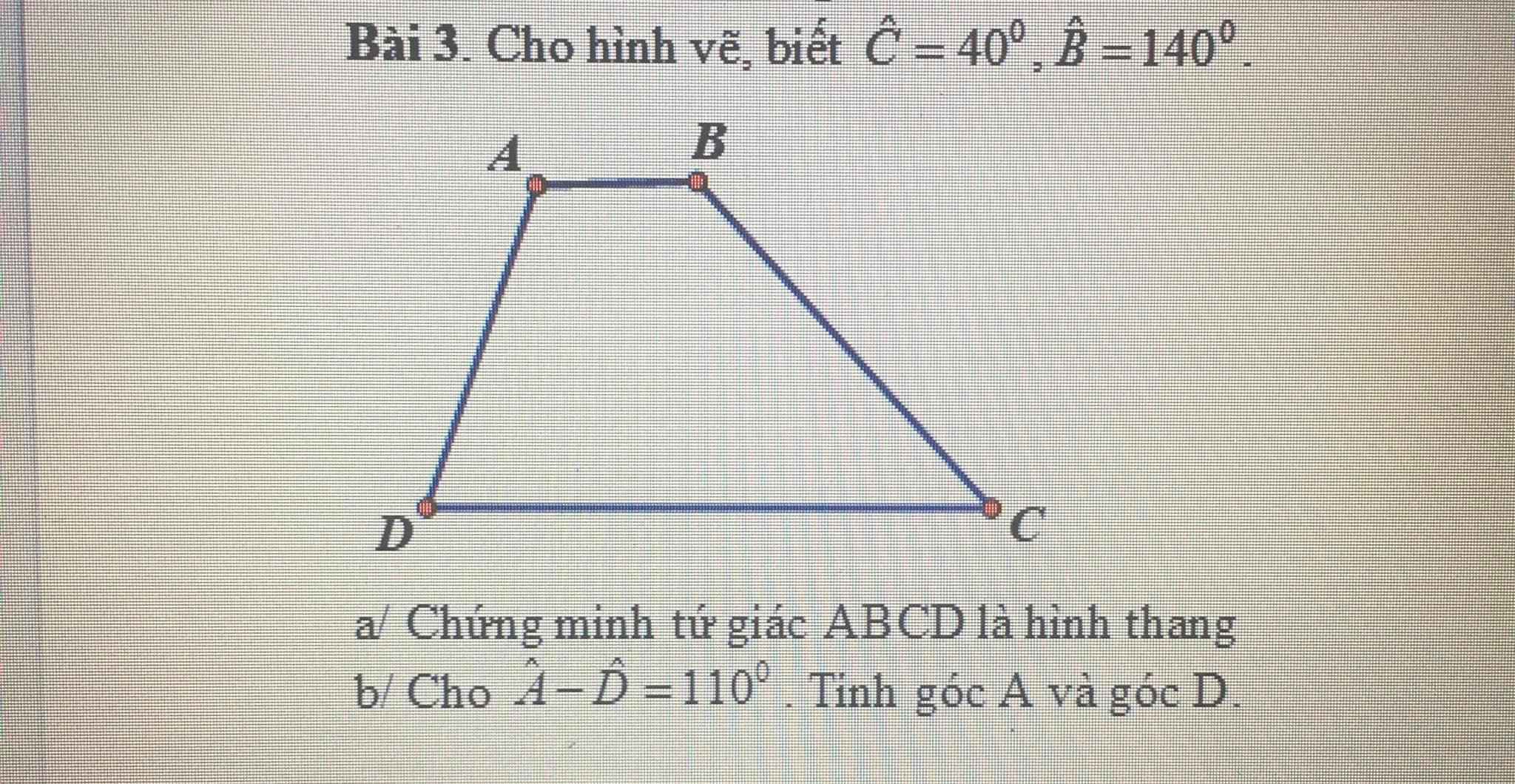
ai giải giúp mình với ạ mình cảm ơn
